题目内容
如图1-8,已知在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)求证:△ABC∽△FCD.
(2)若S△FCD=5,BC=10,求DE的长.
图1-8
(1)证明:∵AD=AC,∴∠ACD=∠ADC.
∵DE⊥BC,BD=DC,∴BE=CE.
∴∠B=∠DCF.
∴△ABC∽△FCD.
(2)解:过点A作AM⊥BC,垂足为M.
由△ABC∽△FCD,BC=2CD,
∴
=(
)2=4.
∴S△ABC=20.
∴20=
×10×AM.
∴AM=4.
又∵DE∥AM,∴
=
.
∵DM=
DC=
,BM=BD+DM,BD=
BC=5,
∴
.∴DE=
.
练习册系列答案
相关题目
某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30．第6小组的频数是7．
某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的 一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30．第6小组的频数是7．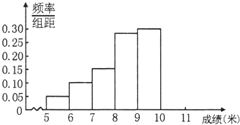
（2012•湛江二模）某市为了解今年高中毕业生的身体素质状况，从本市某校高中毕业班中抽取一个班进行实心球测试，成绩在8米及以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知第一小组为[5，6），从左到右前5个小组的频率分别为0.06，0.10，0.14，0.28，0.30．第6小组的频数是6．