��Ŀ����
17�����ڶ�����R�ϵĺ���f��x����������x0ʹ��$\underset{\underbrace{f��f����f��{x}_{0}������}}{k}$=x0��*��������kΪij�������������x0Ϊ����f��x����һ�����ڵ㣬ʹ�ã�*��ʽ������������k��Ϊx0�����ڣ�ʹ�ã�*��ʽ��������С������k��Ϊx0����С���ڣ�������f��x��=1-|2x-1|������f��x����������| A�� | ǡ��һ����С����Ϊ1�����ڵ㣬ǡ��һ����С����Ϊ2�����ڵ� | |
| B�� | ǡ��һ����С����Ϊ1�����ڵ㣬ǡ��������С����Ϊ2�����ڵ� | |
| C�� | ǡ��������С����Ϊ1�����ڵ㣬ǡ��������С����Ϊ2�����ڵ� | |
| D�� | ǡ��������С����Ϊ1�����ڵ㣬ǡ���ĸ���С����Ϊ2�����ڵ� |
���� ���÷ֶκ�����ʾf��x��������f��x��=x���ⷽ�̿ɵú���f��x��ǡ��������С����Ϊ1�����ڵ㣻�ٽ�f��f��x����д�ɷֶκ�������f��f��x����=x���ⷽ�̿ɵú���f��x��ǡ���ĸ���С����Ϊ2�����ڵ㣮���ɵõ����ۣ�
��� �⣺f��x��=1-|2x-1|=$\left\{\begin{array}{l}{2-2x��x��\frac{1}{2}}\\{2x��x��\frac{1}{2}}\end{array}\right.$��
��f��x��=x����2-2x=x�����x=$\frac{2}{3}$��
��2x=x�����x=0��
������f��x��ǡ��������С����Ϊ1�����ڵ㣻
f��f��x����=1-|2��1-|2x-1|��-1|=$\left\{\begin{array}{l}{4x��x��\frac{1}{4}}\\{2-4x��\frac{1}{4}��x��\frac{1}{2}}\\{4x-2��\frac{1}{2}��x��\frac{3}{4}}\\{4-4x��x��\frac{3}{4}}\end{array}\right.$��
��f��f��x����=x��
��4x=x���ɵ�x=0����2-4x=x�����x=$\frac{2}{5}$��
��4x-2=x�����x=$\frac{2}{3}$����4-4x=x�����x=$\frac{4}{5}$��
���к���f��x��ǡ���ĸ���С����Ϊ2�����ڵ㣮
��ѡD��
���� ���⿼�麯�������ʺ����ã���Ҫ�����¶������������ã�����ֶκ��������ã�ע��ȥ����ֵ�ķ������������������������е��⣮

 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�| A�� | $\frac{31}{16}$ | B�� | $\frac{31}{32}$ | C�� | 31 | D�� | 15 |
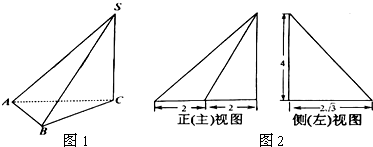
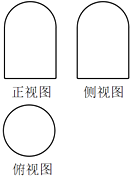 һ�������������ͼ��ͼ������ͼ�Ͳ���ͼ������һ����Բ��һ���߳�Ϊ2����������ɣ�����ͼ��һ��Բ�������������ı����Ϊ7�У�
һ�������������ͼ��ͼ������ͼ�Ͳ���ͼ������һ����Բ��һ���߳�Ϊ2����������ɣ�����ͼ��һ��Բ�������������ı����Ϊ7�У�