题目内容
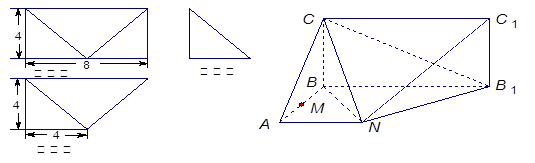
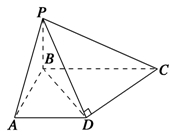
如图,四边形ABCD中, 为正三角形,
为正三角形,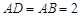 ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为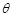 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在 内.
内.
(Ⅰ)求证: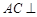 平面PBD;
平面PBD;
(Ⅱ)若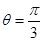 时,求二面角
时,求二面角 的余弦值。
的余弦值。
(1)取BD中点Q,证得Q与O重合。则 面PBD
面PBD
(2)
解析试题分析:(1)取BD中点Q,则 三点共线,即Q与O重合。
三点共线,即Q与O重合。
则 面PBD
面PBD
(2)因为AC 面PBD,而
面PBD,而 面ABCD,所以面ABCD
面ABCD,所以面ABCD 面PBD,则P点在面ABCD上的射影点在交线BD上(即在射线OD上),所以PO与平面ABCD所成的角
面PBD,则P点在面ABCD上的射影点在交线BD上(即在射线OD上),所以PO与平面ABCD所成的角 。以O为坐标原点,OA为
。以O为坐标原点,OA为 轴,OB为
轴,OB为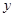 轴建空间直角坐标系。
轴建空间直角坐标系。 ,因为AC
,因为AC 面PBD,所以面PBD的法向量
面PBD,所以面PBD的法向量 ,设面PAB的法向量
,设面PAB的法向量 ,又
,又 ,由
,由 ,得
,得 ①,又
①,又 ,由
,由 ,得
,得 ②, 在①②中令
②, 在①②中令 ,可得
,可得 ,则
,则
所以二面角 的余弦值
的余弦值
考点:本题主要考查立体几何中的垂直关系,角的计算,空间向量的应用。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,将立体问题转化成平面问题,是解决立体几何问题的一个基本思路。通过就落实党的坐标系,利用空间向量,免去了繁琐的逻辑推理过程,对计算能力要求较高。

练习册系列答案
相关题目
已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为( )
| A.x-y=0 | B.x-y+1=0 |
| C.x+y+1=0 | D.x+y=0 |
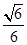 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.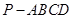 中,
中,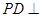 底面
底面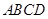 ,底面
,底面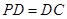 ,
,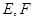 分别是
分别是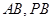 的中点.
的中点.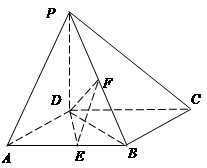
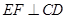 ;
; 内求一点
内求一点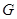 ,使
,使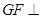 平面
平面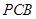 ,并证明你的结论;
,并证明你的结论;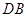 与平面
与平面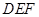 所成角的正弦值.
所成角的正弦值.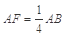 .
.
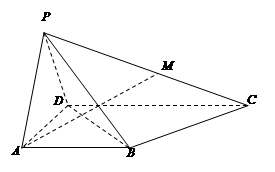
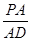 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?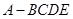 中,
中,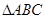 是正三角形,四边形
是正三角形,四边形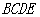 是矩形,且平面
是矩形,且平面 平面
平面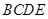 ,
,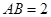 ,
,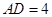 .
.
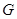 是
是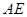 的中点,求证:
的中点,求证: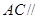 平面
平面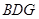 ;
;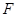 为线段
为线段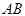 的中点,求二面角
的中点,求二面角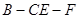 的正切值.
的正切值.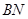 ⊥平面
⊥平面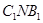 (2)求平面
(2)求平面 与平面
与平面