题目内容
已知直线l丄平面α，直线m?平面β，则“l∥m”是“α⊥β”的（ ）
分析：利用充分条件和必要条件和必要条件的定义进行判断．
解答：解：∵直线l丄平面α，l∥m，
∴m丄平面α，
∵直线m?平面β，∴α⊥β成立．
若α⊥β，当直线l丄平面α时，
则l?β或l∥β，但l∥m，不一定成立，
∴“l∥m”是“α⊥β”的充分条件．
故选：C．
∴m丄平面α，
∵直线m?平面β，∴α⊥β成立．
若α⊥β，当直线l丄平面α时，
则l?β或l∥β，但l∥m，不一定成立，
∴“l∥m”是“α⊥β”的充分条件．
故选：C．
点评：本题主要考查充分条件和必要条件的应用，利用线面垂直和面面垂直的性质和判定定理是解决本题的关键．
练习册系列答案
相关题目
•
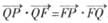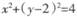的两条切线，分别交x轴于点B、C，当点P的纵坐标y0>4时，试用y0表示线段BC的长，并求ΔPBC面积的最小值.
过点M作
轴于M1,过N作
丄x轴于点N1,
,记点R的轨迹为曲线C。 
的右支相交于P、Q两点（其中点P在第一象限),线段OP交轨迹C于A,若
，
，求直线L的方程