题目内容
（2013•楚雄州模拟）已知点P为△ABC内一点，且
+2
+3
=
，则△APB，△APC，△BPC的面积之比等于（ ）
| PA |
| PB |
| PC |
| 0 |
分析：先将已知向量式化为两个向量共线的形式，再利用平行四边形法则及向量数乘运算的几何意义，三角形面积公式确定面积之比
解答：解：∵
+2
+3
=
，∴
+
=-2
+
），如图：
∵
+
=
=2
，
+
=
=2
∴
=2
∴F、P、G三点共线，且PF=2PG，GF为三角形ABC的中位线
∴
=
=
=
=2
而S△APB=
S△ABC
∴△APB，△APC，△BPC的面积之比等于3：2：1
故选 C
| PA |
| PB |
| PC |
| 0 |
| PA |
| PC |
| (PB |
| PC |
∵
| PA |
| PC |
| PD |
| PF |
| PB |
| PC |
| PE |
| PG |
∴
| PF |
| PG |
∴F、P、G三点共线，且PF=2PG，GF为三角形ABC的中位线
∴
| S△APC |
| S△BPC |
| ||
|
| h1 |
| h2 |
| PF |
| PG |
而S△APB=
| 1 |
| 2 |
∴△APB，△APC，△BPC的面积之比等于3：2：1
故选 C
点评：本题考查了向量式的化简，向量加法的平行四边形法则，向量数乘运算的几何意义等向量知识，充分利用向量共线是解决本题的关键
练习册系列答案
相关题目
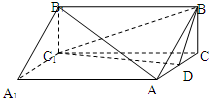（2013•楚雄州模拟）如图，三棱柱ABC-A1B1C1中，AA1⊥面ABC，BC⊥AC，AC=BC=2，AA1=3，D为AC的中点．