题目内容
如图所示，已知E、F分别是正方体ABCD-A1B1C1D1的棱AA1和棱CC1的中点．试判断四边形EBFD1的形状．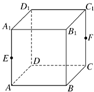
考点：直线与平面平行的性质,平面的基本性质及推论
专题：空间位置关系与距离
分析：根据线面平行的性质结合三角形全等的判定定理以及菱形的判定定理证出即可．
解答：
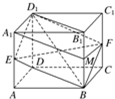解：如图，取BB1的中点M，连接A1M、MF．
∵M、F分别是BB1、CC1的中点，
∴MF∥B1C1．
在正方体ABCD-A1B1C1D1中，有A1D1∥B1C1，
∴M∥A1D1．
∴四边形A1MFD1是平行四边形，
∴A1M∥D1F．
又E、M分别是AA1、BB1的中点，
∴A1E∥BM，
∴四边形A1EBM为平行四边形．∴EB∥A1M．
∴EB∥D1F．
∴四边形EBFD1是平行四边形．
又Rt△EAB≌Rt△FCB，
∴BE=BF，∴四边形EBFD1为菱形．
解：如图，取BB1的中点M，连接A1M、MF．∵M、F分别是BB1、CC1的中点，
∴MF∥B1C1．
在正方体ABCD-A1B1C1D1中，有A1D1∥B1C1，
∴M∥A1D1．
∴四边形A1MFD1是平行四边形，
∴A1M∥D1F．
又E、M分别是AA1、BB1的中点，
∴A1E∥BM，
∴四边形A1EBM为平行四边形．∴EB∥A1M．
∴EB∥D1F．
∴四边形EBFD1是平行四边形．
又Rt△EAB≌Rt△FCB，
∴BE=BF，∴四边形EBFD1为菱形．
点评：本题考查了线面平行的性质，考查了平行四边形的性质以及菱形的判定问题，考查了数形结合，是一道中档题．
练习册系列答案
相关题目
下列各个说法正确的是（ ）
| A、终边相同的角都相等 |
| B、钝角是第二象限的角 |
| C、第一象限的角是锐角 |
| D、第四象限的角是负角 |
下列选项中，p是q的必要不充分条件的是（ ）
| A、p：a+c＞b+d，q：a＞b且c＞d |
| B、p：a＞1，b＞1 q：f（x）=ax-b（1≠a＞0）的图象不过第二象限 |
| C、p：x=1，q：x2=x |
| D、p：a＞1，q：f（x）=logax（1≠a＞0）在（0，+∞）上为增函数 |