题目内容
5．若x，y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{3x+y-3≤0}\\{y≥0}\end{array}\right.$，则$\frac{y}{x+2}$的取值范围是[0，$\frac{3}{5}$]．分析 作出不等式组对应的平面区域，利用$\frac{y}{x+2}$的几何意义进行求解即可．
解答 解：作出不等式组对应的平面区域如图，
设k=$\frac{y}{x+2}$，则k的几何意义为区域内的点到定点D（-2，0）的斜率，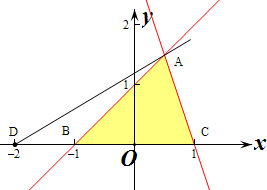
由图象知：
AD的斜率最大，DC的斜率最小，最小为0，
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x+y-3=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$，即A（$\frac{1}{2}$，$\frac{3}{2}$），
即AD的斜率k=$\frac{\frac{3}{2}}{\frac{1}{2}+2}$=$\frac{3}{5}$，
故0≤$\frac{y}{x+2}$≤$\frac{3}{5}$，
故答案为：[0，$\frac{3}{5}$]．
点评 本题主要考查线性规划的应用，根据目标函数的几何意义以及直线斜率公式是解决本题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
16．设集合M={x|2x2-y2=1}，N={y|y=x2}，则M∩N=（ ）
| A． | {（1，1）} | B． | {（-1，1），（1，1）} | C． | $[{\frac{1}{2}，+∞}）$ | D． | $[{\frac{{\sqrt{2}}}{2}，+∞}）$ |
13．若（2x-1）2015=a0+a1x+a2x2+…+a2015x2015（x∈R），则$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2015}}}}{{{2^{2015}}{a_1}}}$的值为（ ）
| A． | $\frac{1}{2015}$ | B． | -$\frac{1}{2015}$ | C． | $\frac{1}{4030}$ | D． | -$\frac{1}{4030}$ |
20．知a1=1，an+1=$\frac{a_n}{{3{a_n}+1}}$，则数列{an}的通项为an=（ ）
| A． | $\frac{1}{2n-1}$ | B． | 2n-1 | C． | $\frac{1}{3n-2}$ | D． | 3n-2 |
17．
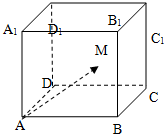如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |