题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中 的图象与x轴的交点中,相邻两个交点之间的距离为
的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为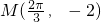 .
.
(1)求f(x)的解析式;
(2)当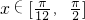 时,求f(x)的最大值及相应的x的值.
时,求f(x)的最大值及相应的x的值.
解:(1)由题意得A=2,周期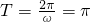 ,得ω=2,此时f(x)=2sin(2x+φ),
,得ω=2,此时f(x)=2sin(2x+φ),
将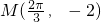 代入上式得
代入上式得 ,
,
即 ,
,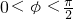 ,
,
解得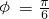 ,所以f(x)=
,所以f(x)= ;
;
(2)因为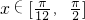 ,所以
,所以 ,
,
所以,当且仅当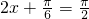 ,即
,即 时,
时,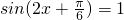 ,
,
即有f(x)的最大值为2.
分析:(1)由题意得A=2,由周期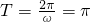 ,可求ω,则有f(x)=2sin(2x+φ),然后将
,可求ω,则有f(x)=2sin(2x+φ),然后将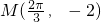 代入结合已知
代入结合已知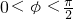 ,可求
,可求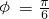 ,从而可求函数f(x)
,从而可求函数f(x)
(2)由x的范围可求2x+ 的范围,结合正弦型函数的性质可求函数函数的最大值
的范围,结合正弦型函数的性质可求函数函数的最大值
点评:本题主要考查三角函数的图象与性质,考查运算求解的能力.
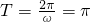 ,得ω=2,此时f(x)=2sin(2x+φ),
,得ω=2,此时f(x)=2sin(2x+φ),将
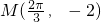 代入上式得
代入上式得 ,
,即
 ,
,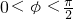 ,
,解得
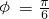 ,所以f(x)=
,所以f(x)= ;
;(2)因为
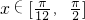 ,所以
,所以 ,
,所以,当且仅当
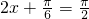 ,即
,即 时,
时,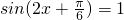 ,
,即有f(x)的最大值为2.
分析:(1)由题意得A=2,由周期
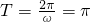 ,可求ω,则有f(x)=2sin(2x+φ),然后将
,可求ω,则有f(x)=2sin(2x+φ),然后将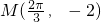 代入结合已知
代入结合已知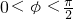 ,可求
,可求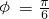 ,从而可求函数f(x)
,从而可求函数f(x)(2)由x的范围可求2x+
 的范围,结合正弦型函数的性质可求函数函数的最大值
的范围,结合正弦型函数的性质可求函数函数的最大值点评:本题主要考查三角函数的图象与性质,考查运算求解的能力.

练习册系列答案
相关题目