题目内容
ω为正实数,函数 在
在 上为增函数,则( )
上为增函数,则( )A.0<ω≤

B.0<ω≤2
C.0<ω≤

D.ω≥2
【答案】分析:根据题意可得:f(x)= ,所以可得函数的单调区间,进而结合函数在
,所以可得函数的单调区间,进而结合函数在 上为增函数,可得答案.
上为增函数,可得答案.
解答:解:因为函数 ,
,
所以 =
= ,
,
所以函数的单调增区间为: ,
,
又因为函数在 上为增函数,
上为增函数,
所以 ,解得ω≤
,解得ω≤ ,
,
因为ω为正实数,所以0<ω≤ .
.
故选A.
点评:本题主要考查正弦函数的单调性.
 ,所以可得函数的单调区间,进而结合函数在
,所以可得函数的单调区间,进而结合函数在 上为增函数,可得答案.
上为增函数,可得答案.解答:解:因为函数
 ,
,所以
 =
= ,
,所以函数的单调增区间为:
 ,
,又因为函数在
 上为增函数,
上为增函数,所以
 ,解得ω≤
,解得ω≤ ,
,因为ω为正实数,所以0<ω≤
 .
.故选A.
点评:本题主要考查正弦函数的单调性.

练习册系列答案
相关题目
 、
、 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为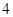 ,则
,则 在
在 上的最小值为
.
上的最小值为
. ,
, 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为 ,则
,则 在
在 上的最小值为 .
上的最小值为 . 在
在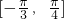 上为增函数,则
上为增函数,则
