题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且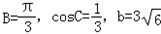 .
.
(I)求c的值;
(II)求△ABC的面积.
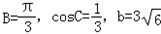 .
.(I)求c的值;
(II)求△ABC的面积.
解:(I)∵cosC= ,且C为三角形的内角,
,且C为三角形的内角,
∴sinC=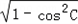 =
=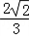 ,又B=
,又B=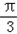 ,b=3
,b=3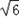 ,
,
∴根据正弦定理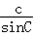 =
=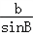
得:c=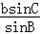 =8;
=8;
II)∵cosC= ,b=3
,b=3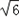 ,c=8,
,c=8,
∴根据余弦定理c2=a2+b2﹣2abcosC
得:64=a2+54﹣2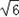 a,
a,
即a2﹣2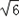 a﹣10=0,
a﹣10=0,
解得:a=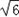 +4或a=
+4或a=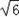 ﹣4(舍去),
﹣4(舍去),
则△ABC的面积S= acsinB=
acsinB= ×(
×(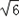 +4)×8×
+4)×8×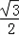
=6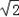 +8
+8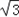 .
.
 ,且C为三角形的内角,
,且C为三角形的内角,∴sinC=
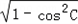 =
=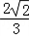 ,又B=
,又B=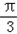 ,b=3
,b=3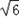 ,
,∴根据正弦定理
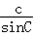 =
=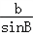
得:c=
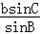 =8;
=8;II)∵cosC=
 ,b=3
,b=3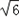 ,c=8,
,c=8,∴根据余弦定理c2=a2+b2﹣2abcosC
得:64=a2+54﹣2
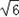 a,
a,即a2﹣2
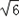 a﹣10=0,
a﹣10=0,解得:a=
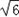 +4或a=
+4或a=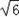 ﹣4(舍去),
﹣4(舍去),则△ABC的面积S=
 acsinB=
acsinB= ×(
×(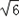 +4)×8×
+4)×8×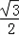
=6
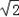 +8
+8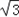 .
.
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |