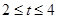题目内容
定义域为R的函数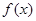 满足
满足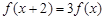 ,当
,当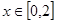 时,
时,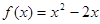 ,若
,若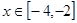 时,
时,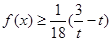 恒成立,则实数
恒成立,则实数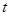 的取值范围是 .
的取值范围是 .
A.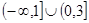 B.
B.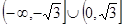
C.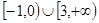 D.
D.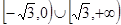
【答案】
C
【解析】
试题分析:因为 ,所以
,所以 ,所以当
,所以当 时,
时, ,所以
,所以 ,所以函数
,所以函数 在
在 上的最小值为
上的最小值为 ,所以要使
,所以要使 时,
时, 恒成立,只需
恒成立,只需 。
。
考点:函数性质的综合应用;函数解析式的求法;分式不等式的解法。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: 在
在 上恒成立
上恒成立 ;思路2:
;思路2:  在
在 上恒成立
上恒成立 。
。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
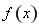
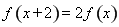
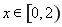
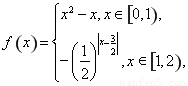
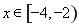
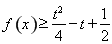
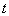
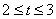
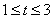
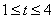
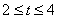
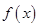 满足
满足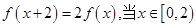 时,
时,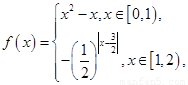 若
若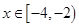 时,
时,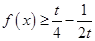 恒成立,则实数
恒成立,则实数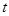 的取值范围是( )
的取值范围是( )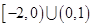 B.
B.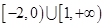
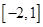 D.
D.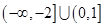
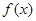 满足:
满足: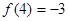 ,且对任意
,且对任意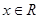 总有
总有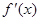 <3,则不等式
<3,则不等式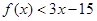 的解集为( )
的解集为( )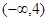 B.
B.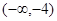 C.
C.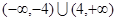 D.
D.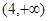
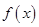 满足
满足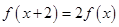 ,当
,当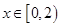 时,
时,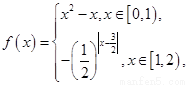 则当
则当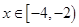 时,函数
时,函数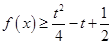 恒成立,则实数
恒成立,则实数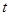 的取值范围为( )
的取值范围为( ) 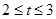 B.
B.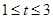 C.
C.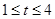 D.
D.