题目内容
2.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且椭圆C与直线$\sqrt{2}$x-$\sqrt{5}$y-3$\sqrt{2}$=0相切,直线l:y=kx-3与椭圆C交于不同的两点A,B.(1)求椭圆C的方程;
(2)求以AB为直径的圆过椭圆的右焦点时直线l的方程.
分析 (1)运用离心率公式和a,b,c的关系,将直线$\sqrt{2}$x-$\sqrt{5}$y-3$\sqrt{2}$=0代入椭圆方程,运用判别式为0,可得a,b,进而得到椭圆方程;
(2)y=kx-3代入椭圆方程x2+2y2=10,运用判别式大于0,韦达定理,结合直径所对的圆周角为直角,运用向量的数量积的坐标表示,即可得到斜率k,进而得到直线方程.
解答 解:(1)由e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
可设a=2t,b=c=$\sqrt{2}$t,
则椭圆方程为x2+2y2=4t2,
直线$\sqrt{2}$x-$\sqrt{5}$y-3$\sqrt{2}$=0代入椭圆方程,可得
$\frac{9}{5}$x2-$\frac{12\sqrt{2}}{\sqrt{5}}$x+18-4t2=0,
由直线和椭圆相切,可得判别式为0,
即为$\frac{144×2}{5}$-4×$\frac{9}{5}$×(18-4t2)=0,
解得t=$\frac{\sqrt{10}}{2}$,
即有a=$\sqrt{10}$,b=$\sqrt{5}$,
则椭圆方程为$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{5}$=1;
(2)由y=kx-3代入椭圆方程x2+2y2=10,
可得(1+2k2)x2-12kx+8=0,
设A(x1,y1),B(x2,y2),
判别式为144k2-32(1+2k2)>0,
解得k2>$\frac{2}{5}$.
x1+x2=$\frac{12k}{1+2{k}^{2}}$,x1x2=$\frac{8}{1+2{k}^{2}}$,
以AB为直径的圆过椭圆的右焦点F($\sqrt{5}$,0).
即有$\overrightarrow{AF}$⊥$\overrightarrow{BF}$=0,即为$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,
(x1-$\sqrt{5}$)(x2-$\sqrt{5}$)+y1y2=0,
即为x1x2+5-$\sqrt{5}$(x1+x2)+(kx1-3)(kx2-3)=0,
即有(1+k2)x1x2-($\sqrt{5}$+3k)(x1+x2)+14=0,
即为(1+k2)•$\frac{8}{1+2{k}^{2}}$-($\sqrt{5}$+3k)•$\frac{12k}{1+2{k}^{2}}$+14=0,
解得k=$\frac{11\sqrt{5}}{30}$,k2>$\frac{2}{5}$.成立.
即有直线l的方程为y=$\frac{11\sqrt{5}}{30}$x-3.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用判别式和韦达定理,考查运算能力,属于中档题.

| A. | 零向量是唯一没有方向的向量 | |
| B. | 平面内的单位向量有且仅有一个 | |
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$是共线向量,$\overrightarrow{b}$与$\overrightarrow{c}$是平行向量,则$\overrightarrow{a}$与$\overrightarrow{c}$是方向相同的向量 | |
| D. | 相等的向量必是共线向量 |
| A. | 命题“若x<1,则-≤x≤1”的逆否命题是“若x≥1,则x<-1或x≥1” | |
| B. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex≤0” | |
| C. | “a>0”是“函数f(x)=|(ax-1)x|在区间(-∞,0)上单调递减”的充要条件 | |
| D. | 已知命题p:?x∈R,lnx<lgx;命题q:?x0∈R,x03=1-x02,则“(¬p)∨(¬q)为真命题”. |
| A. | 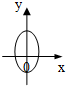 | B. | 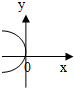 | C. | 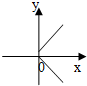 | D. | 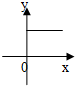 |
| A. | a2+a10>2a6 | B. | a2+a10<2a6 | ||
| C. | a2+a10=2a6 | D. | a2+a10与2a6的大小与a有关 |