题目内容
已知A、B、C是平面上任意三点，BC=a，CA=b，AB=c，则
的最小值是________．
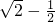
分析：先将函数变形，并化简，再利用基本不等式，即可求得结论．
解答：依题意，得b+c≥a，于是
=
=
≥
=
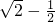
≥其中，等号当且仅当b+c=a且
，即a=
，b=
时成立．所以，所求最小值为
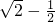
故答案为：
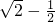
点评：本题考查基本不等式的运用，解题的关键是化简函数，并利用基本不等式求最值，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知A、B、C是平面内不共线的三点，P为平面内的动点，且
=
+λ(
+
) (λ＞0)，则P的轨迹过△ABC的（ ）
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|
| A、重心 | B、垂心 | C、内心 | D、外心 |
已知A、B、C是平面上不共线的三点，O是三角形ABC的重心，动点P满足
=
(
+
+2
)，则点P一定为三角形ABC的（ ）
| OP |
| 1 |
| 3 |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| OC |
| A、AB边中线的中点 |
| B、AB边中线的三等分点（非重心） |
| C、重心 |
| D、AB边的中点 |