题目内容
已知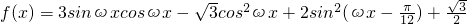 (其中ω>0)的最小正周期为π.
(其中ω>0)的最小正周期为π.
(1)求f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知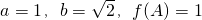 ,求角C.
,求角C.
解:(1) =
= =
= ∵T=π,ω>0,∴
∵T=π,ω>0,∴ ∴
∴
故递增区间为
(2)∴ ∵
∵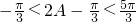 ∴
∴
即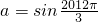 或
或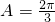
又a<b,∴A<B,故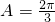 舍去,∴
舍去,∴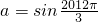 .
.
由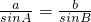 得
得 ,∴
,∴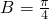 或
或 ,
,
若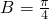 ,则
,则 .
.
若 ,则
,则 .
.
注意:没有说明“∵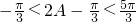 ”扣(2分)
”扣(2分)
分析:(1)利用二倍角公式、两角差的余弦函数展开,合并后,化为一个角的一个三角函数的形式,利用周期求出ω,结合正弦函数的单调增区间,求出函数的单调增区间.
(2)通过f(A)=1,求出A的值,利用正弦定理求出B,C.
点评:本题是中档题,考查三角函数的化简求值,三角函数公式的灵活运应,正弦定理的应用,注意A的范围是确定A的大小的根据,考查计算能力,逻辑推理能力.
 =
= =
= ∵T=π,ω>0,∴
∵T=π,ω>0,∴ ∴
∴
故递增区间为

(2)∴
 ∵
∵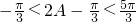 ∴
∴
即
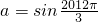 或
或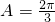
又a<b,∴A<B,故
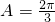 舍去,∴
舍去,∴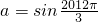 .
.由
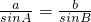 得
得 ,∴
,∴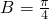 或
或 ,
,若
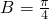 ,则
,则 .
.若
 ,则
,则 .
.注意:没有说明“∵
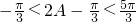 ”扣(2分)
”扣(2分)分析:(1)利用二倍角公式、两角差的余弦函数展开,合并后,化为一个角的一个三角函数的形式,利用周期求出ω,结合正弦函数的单调增区间,求出函数的单调增区间.
(2)通过f(A)=1,求出A的值,利用正弦定理求出B,C.
点评:本题是中档题,考查三角函数的化简求值,三角函数公式的灵活运应,正弦定理的应用,注意A的范围是确定A的大小的根据,考查计算能力,逻辑推理能力.

练习册系列答案
相关题目
 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 (其中A>0,
(其中A>0, )的图象如图所示.
)的图象如图所示. ,求
,求 的值.
的值.
 其中a>0.
其中a>0.
 其中
其中 ,若
,若 ∥
∥ ,则
,则 的值是
的值是 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;