题目内容
设数列{an}的前n项和为Sn,且对于任意n∈N*,都有![]() 成立,则an= .
成立,则an= .
考点:
数列的概念及简单表示法.
专题:
等差数列与等比数列.
分析:
利用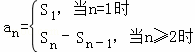 即可得出.
即可得出.
解答:
解:当n=1时,![]() ;
;
当n≥2时,an=Sn﹣Sn﹣1=2n+n﹣1﹣(2n﹣1+n﹣1﹣1)=2n﹣1+1.
上式对于n=1时也成立.
∴![]() .
.
故答案为2n﹣1+1.
点评:
熟练掌握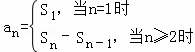 是解题的关键.
是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
题目内容
设数列{an}的前n项和为Sn,且对于任意n∈N*,都有![]() 成立,则an= .
成立,则an= .
考点:
数列的概念及简单表示法.
专题:
等差数列与等比数列.
分析:
利用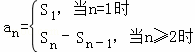 即可得出.
即可得出.
解答:
解:当n=1时,![]() ;
;
当n≥2时,an=Sn﹣Sn﹣1=2n+n﹣1﹣(2n﹣1+n﹣1﹣1)=2n﹣1+1.
上式对于n=1时也成立.
∴![]() .
.
故答案为2n﹣1+1.
点评:
熟练掌握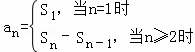 是解题的关键.
是解题的关键.

 步步高达标卷系列答案
步步高达标卷系列答案