题目内容
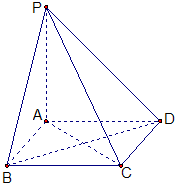
如图,四棱锥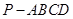 的底面
的底面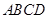 是矩形,
是矩形,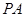 ⊥平面
⊥平面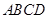 ,
,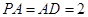 ,
,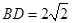 .
.
(1)求证: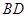 ⊥平面
⊥平面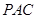 ;
;
(2)求二面角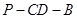 余弦值的大小;
余弦值的大小;
(3)求点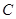 到平面
到平面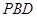 的距离.
的距离.
(1) 见解析(2)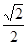 (3)
(3)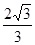
解析试题分析:(1)证明:∵底面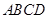 是矩形,
是矩形, ,
,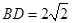 ,
,
∴底面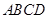 是正方形,∴
是正方形,∴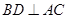 .
.
∵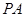 ⊥平面
⊥平面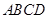 ,
,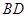
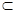 平面
平面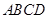 ,∴
,∴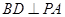 .
.
∵ P平面
P平面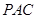 ,
, ,∴
,∴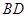 ⊥平面
⊥平面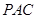 .
.
(2)解:∵底面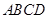 是正方形,∴
是正方形,∴ .
.
又∵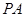 ⊥平面
⊥平面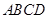 ,∴
,∴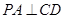 .
.
∵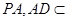 P平面
P平面 ,
,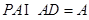 ,∴
,∴ ⊥平面
⊥平面 ,
,
∴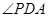 为二面角
为二面角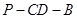 的平面角.
的平面角.
在 中,
中,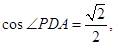 即求二面角
即求二面角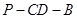 余弦值为
余弦值为
(3)解:设点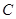 到平面
到平面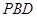 的距离为
的距离为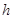 ,所以
,所以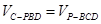 ,
,
所以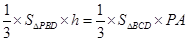 ,即
,即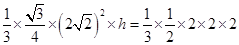 ,解得
,解得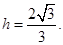
即点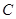 到平面
到平面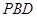 的距离为
的距离为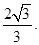
考点:本小题主要考查线面垂直的证明、二面角的求法和等体积法求高,考查了学生的空间想象能力、逻辑推理能力和运算求解能力.
点评:证明线面、面面间的位置关系时,要紧扣判定定理,要注意灵活运用性质定理和判定定理,把定理要求的条件一一列举出来,缺一不可.求二面角时,要先证后求,不能只求不证.求点到平面的距离时,等体积法是常用的方法.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 ,且
,且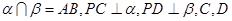 是垂足,
是垂足,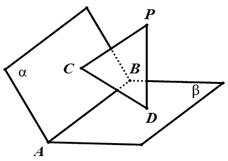
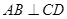
 中,底面
中,底面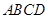 是直角梯形,
是直角梯形,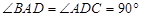 ,
, ,
,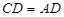 .
.
 是二面角
是二面角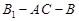 的平面角;
的平面角; 上是否存一点
上是否存一点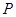 ,使得
,使得 与平面
与平面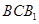 与平面
与平面 都平行?证明你的结论.
都平行?证明你的结论.
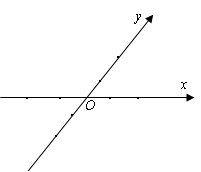
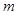 ),则该几何体的体积。
),则该几何体的体积。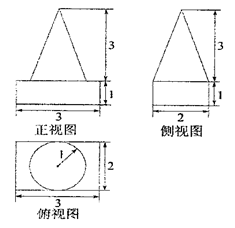
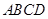 满足
满足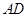 ∥
∥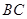 ,
,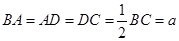 ,
,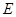 是
是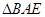 沿着
沿着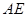 翻折成
翻折成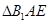 ,使面
,使面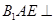 面
面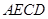 ,
, 为
为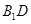 的中点.
的中点. 
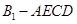 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: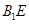 ∥面
∥面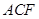 ;
;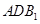 与面
与面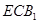 所成二面角的余弦值.
所成二面角的余弦值.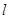 经过平面
经过平面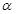 内一定点
内一定点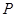 ,但
,但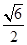 求二面角E-AF-C的余弦值
求二面角E-AF-C的余弦值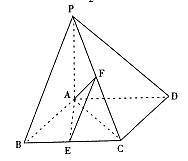
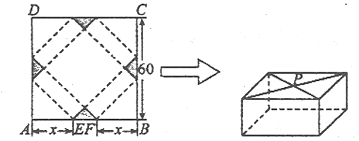
 图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(
图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x( cm).
cm).