Question

（2012•长宁区二模）知向量

OB

=(2，0)，|

CA

|=

2

，

OC

=（2，2），则

OA

与

OB

夹角的最小值和最大值依次是（　　）

• A．0，

  π

  4

• B．

  π

  4

  ，

  5π

  12

• C．

  π

  12

  ，

  5π

  12

• D．

  5π

  12

  ，

  π

  2

Answer 1

分析：由题意知，点A在以C（2，2）为圆心，以

2

为半径的圆上，所以本题应采用数形结合来解题，由图来分析其夹角的最大最小值点．

解答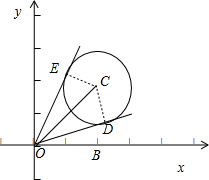：解：由题意知，点A在以C（2，2）为圆心，以

2

为半径的圆上，如图所示，OD，OE为圆的切线，
在△COD中，OC=2

2

，CD=

2

，∠CDO=

π

2

，所以∠COD=

π

6

．
又因为∠COB=

π

4

，所以当A在D处时，则

OA

与

OB

夹角的最小值为

π

4

-

π

6

=

π

12

，

OA

与

OB

夹角的最大值

π

4

+

π

6

=

5π

12

，
故选C．

点评：本题考查向量的坐标运算及向量的数量积与夹角，是一道考查基本功的题，属于中档题．