题目内容
已知定义在R上的函数f(x)的图象关于点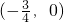 对称,且满足
对称,且满足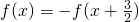 ,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2006)的值为______.
,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2006)的值为______.
解:∵函数f(x)满足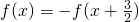 ,
,
∴f(x+3)=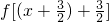 =
=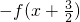 =f(x)
=f(x)
即f(x)是一个以3为周期的周期函数
又∵函数f(x)的图象关于点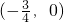 对称,
对称,
∴f(x)=-f( -x),又函数f(x)满足
-x),又函数f(x)满足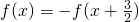 ,
,
∴f( -x)=
-x)=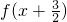
即f(x)=f(-x)
故函数f(x)为定义在R上的偶函数
又∵f(-1)=1,f(0)=-2,
∴f(1)=f(-1)=f(2)=1
∴f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z
∴f(1)+f(2)+…+f(2006)=f(1)+f(2)=1+1=2
故答案为2
分析:由已知中定义在R上的函数f(x)的图象关于点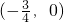 对称,且满足
对称,且满足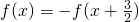 ,f(-1)=1,f(0)=-2,我们可得f(x)是一个以3为周期的周期函数,且f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z,然后利用分组分解法,我们可以将f(1)+f(2)+…+f(2006)转化为f(1)+f(2),进而得到答案.
,f(-1)=1,f(0)=-2,我们可得f(x)是一个以3为周期的周期函数,且f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z,然后利用分组分解法,我们可以将f(1)+f(2)+…+f(2006)转化为f(1)+f(2),进而得到答案.
点评:本题考查的知识点是函数的周期性,奇偶函数图象的对称性,其中根据已知条件确定出函数的周期,及一个周期中各整数对应的函数值,是解答本题的关键.
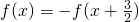 ,
,∴f(x+3)=
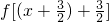 =
=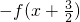 =f(x)
=f(x)即f(x)是一个以3为周期的周期函数
又∵函数f(x)的图象关于点
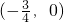 对称,
对称,∴f(x)=-f(
 -x),又函数f(x)满足
-x),又函数f(x)满足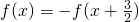 ,
,∴f(
 -x)=
-x)=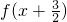
即f(x)=f(-x)
故函数f(x)为定义在R上的偶函数
又∵f(-1)=1,f(0)=-2,
∴f(1)=f(-1)=f(2)=1
∴f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z
∴f(1)+f(2)+…+f(2006)=f(1)+f(2)=1+1=2
故答案为2
分析:由已知中定义在R上的函数f(x)的图象关于点
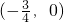 对称,且满足
对称,且满足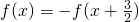 ,f(-1)=1,f(0)=-2,我们可得f(x)是一个以3为周期的周期函数,且f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z,然后利用分组分解法,我们可以将f(1)+f(2)+…+f(2006)转化为f(1)+f(2),进而得到答案.
,f(-1)=1,f(0)=-2,我们可得f(x)是一个以3为周期的周期函数,且f(3k)=-2,f(3k+1)=1,f(3k+2)=1,k∈Z,然后利用分组分解法,我们可以将f(1)+f(2)+…+f(2006)转化为f(1)+f(2),进而得到答案.点评:本题考查的知识点是函数的周期性,奇偶函数图象的对称性,其中根据已知条件确定出函数的周期,及一个周期中各整数对应的函数值,是解答本题的关键.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |