题目内容
已知 和
和 都是锐角,且
都是锐角,且 ,
, ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
C
解析试题分析:因为已知中, 和
和 都是锐角,且
都是锐角,且 ,
, ,那么则
,那么则
由于 和
和 都是锐角,则和角为小于
都是锐角,则和角为小于 ,而余弦值为负数,说明为钝角,因此可知其正弦值为
,而余弦值为负数,说明为钝角,因此可知其正弦值为 ,
, ,代入上式可知值为
,代入上式可知值为 ,选C.
,选C.
考点:本试题考查了三角函数的恒等变形运用。
点评:解决该试题的关键是能够合理的运用凑角的思想来表示未知角,运用已知角的和或者差来得到角的关系,然后结合两角和差的公式来求求解得到。易错点就是对于同角关系式中平方关系的运用,注意符号的唯一性问题,属于中档题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知 ,则
,则 ( )
( )
| A.-2 | B.2 | C. | D.- |
函数
 的图象如图所示,为得到函数
的图象如图所示,为得到函数 的图象,可将
的图象,可将 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
函数 对任意的
对任意的 都有
都有 成立,则
成立,则 的最小值为
的最小值为  ( )
( )
A.  | B.1 | C.2 | D.4 |
已知 且
且 ,则角
,则角 在( )
在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若 ,则
,则
A. | B. | C. | D. |
设 是正实数,函数
是正实数,函数 在
在 上是增函数,那么
上是增函数,那么 的最大值是
的最大值是
A. | B.2 | C. | D.3 |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
 的图像与x轴的交点的横坐标构成一个公差为
的图像与x轴的交点的横坐标构成一个公差为 的等差数列,要得到函数
的等差数列,要得到函数 的图像,只需将
的图像,只需将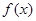 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移