题目内容
(本小题满分12分)
已知函数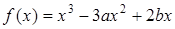 在
在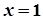 处有极小值
处有极小值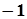 .
.
(1)求函数 的单调区间;
的单调区间;
(2)求函数 在闭区间
在闭区间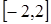 上的最大值和最小值.
上的最大值和最小值.
【答案】
解:(1)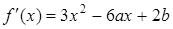 ,
, 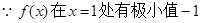

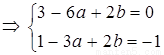 解得
解得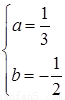 3分
3分
所以 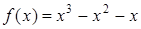 ,
,
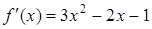 4分
4分
令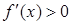 ,解得
,解得 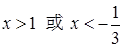 ;
;
令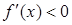 ,解得
,解得 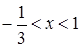
所以 函数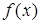 的单调递增区间是
的单调递增区间是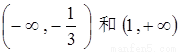 ,单调递减区间是
,单调递减区间是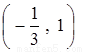
6分
(2)由(1)知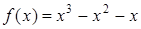 ,
, 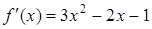
令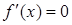 ,解得
,解得 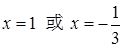 ; 8分
; 8分
由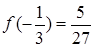 ,
,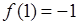 , 又
, 又 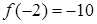 ,
,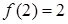 10分
10分
导数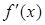 的正负以及
的正负以及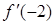 ,
,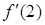 如下表所示:
如下表所示:
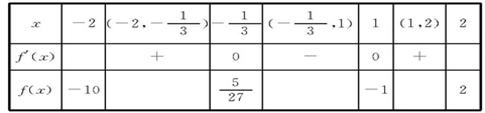
由表中数据知,函数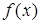 最大值为
最大值为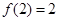 ,最小值
,最小值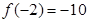 .
.
所以函数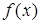 在闭区间[-2,2]上的最大值为2,最小值为-10 . 12分
在闭区间[-2,2]上的最大值为2,最小值为-10 . 12分
【解析】略

练习册系列答案
相关题目