题目内容
直线l:y=kx-1与双曲线c:2x2-y2=1的左支交于不同的两点,那么k的取值范围是( )A.(
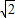 ,2)
,2)B.(-
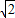 ,
,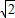 )
)C.(-2,2)
D.(-2,-
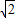 )
)
【答案】分析:直接联立直线方程和双曲线方程,化为关于x的一元二次方程后由判别式大于0,两根之和小于0,两根之积大于0联立不等式组求解k的取值范围.
解答:解:由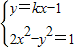 ,得(2-k2)x2+2kx-2=0.
,得(2-k2)x2+2kx-2=0.
要使y=kx-1与双曲线c:2x2-y2=1的左支交于不同的两点,
则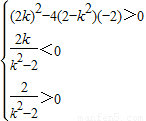 ,即
,即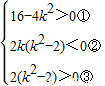 ,
,
解①得,-2<k<2.
解②得,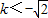 或0<k<
或0<k<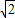 .
.
解③得,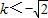 或k>
或k>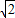 .
.
所以-2<k<-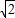 .
.
故选D.
点评:本题考查了直线与圆锥曲线的关系,考查了直线与双曲线的交点问题,考查了数学转化思想方法,关键是由题意列出不等式组,是中档题.
解答:解:由
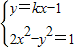 ,得(2-k2)x2+2kx-2=0.
,得(2-k2)x2+2kx-2=0.要使y=kx-1与双曲线c:2x2-y2=1的左支交于不同的两点,
则
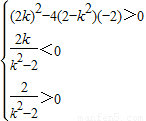 ,即
,即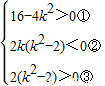 ,
,解①得,-2<k<2.
解②得,
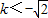 或0<k<
或0<k<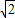 .
.解③得,
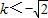 或k>
或k>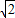 .
.所以-2<k<-
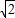 .
.故选D.
点评:本题考查了直线与圆锥曲线的关系,考查了直线与双曲线的交点问题,考查了数学转化思想方法,关键是由题意列出不等式组,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目