题目内容
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f'(x)是函数y=f(x)的导数,f''是f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若 ,请你根据这一发现,求:
,请你根据这一发现,求:
(1)函数 对称中心为________;
对称中心为________;
(2)计算 =________.
=________.
解:(1)依题意,得:f′(x)=x2-x+3,∴f″(x)=2x-1.
由f″(x)=0,即2x-1=0.
∴x= ,
,
又 f( )=1,
)=1,
∴函数 的对称中心为(
的对称中心为( ,1);
,1);
(2)由(1)知,若(a,b)与(c,d)为f(x)图象上的点,且关于点( ,1)对称,则有a+c=1,且f(a)+f(c)=2,
,1)对称,则有a+c=1,且f(a)+f(c)=2,
设S= ,
,
又S=f( )+f(
)+f( )+f(
)+f(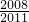 )+f(
)+f( )+…+f(
)+…+f( ),
),
所以2S=[f( )+f(
)+f( )]+…+[f(
)]+…+[f( )+f(
)+f( )]=2×2010,
)]=2×2010,
所以S=2010,即 =2010.
=2010.
故答案为:(1)( ,1);(2)2010.
,1);(2)2010.
分析:(1)先求f′(x)得解析式,再求f″(x),由f″(x)=0 求得拐点的横坐标,代入函数解析式求拐点的纵坐标.
(2)由(1)知,若(a,b)与(c,d)为f(x)图象上的点,且关于点( ,1)对称,则有a+c=1,且f(a)+f(c)=2,根据该结论即可求得答案;
,1)对称,则有a+c=1,且f(a)+f(c)=2,根据该结论即可求得答案;
点评:本题考查一阶导数、二阶导数的求法,函数的拐点的定义以及函数图象关于某点对称的条件.
由f″(x)=0,即2x-1=0.
∴x=
 ,
,又 f(
 )=1,
)=1,∴函数
 的对称中心为(
的对称中心为( ,1);
,1);(2)由(1)知,若(a,b)与(c,d)为f(x)图象上的点,且关于点(
 ,1)对称,则有a+c=1,且f(a)+f(c)=2,
,1)对称,则有a+c=1,且f(a)+f(c)=2,设S=
 ,
,又S=f(
 )+f(
)+f( )+f(
)+f(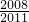 )+f(
)+f( )+…+f(
)+…+f( ),
),所以2S=[f(
 )+f(
)+f( )]+…+[f(
)]+…+[f( )+f(
)+f( )]=2×2010,
)]=2×2010,所以S=2010,即
 =2010.
=2010.故答案为:(1)(
 ,1);(2)2010.
,1);(2)2010.分析:(1)先求f′(x)得解析式,再求f″(x),由f″(x)=0 求得拐点的横坐标,代入函数解析式求拐点的纵坐标.
(2)由(1)知,若(a,b)与(c,d)为f(x)图象上的点,且关于点(
 ,1)对称,则有a+c=1,且f(a)+f(c)=2,根据该结论即可求得答案;
,1)对称,则有a+c=1,且f(a)+f(c)=2,根据该结论即可求得答案;点评:本题考查一阶导数、二阶导数的求法,函数的拐点的定义以及函数图象关于某点对称的条件.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目