题目内容
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面 均为等边三角形,
均为等边三角形, ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.

解:(Ⅰ)由题设

 ,连结
,连结 ,
, 为等腰直角三角形,
为等腰直角三角形,
所以 ,且
,且 ,又
,又 为等腰三角形,
为等腰三角形,
 ,且
,且 ,从而
,从而 .
.
所以 为直角三角形,
为直角三角形, .
.
又 . 所以
. 所以 平面
平面
(Ⅱ)解法一:取 中点
中点 ,连结
,连结 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,
得 .
. 为二面角
为二面角 的平面角.
的平面角.
由 得
得 平面
平面 .
.
 所以
所以 ,又
,又 ,
,
故 .
.
所以二面角 的余弦值为
的余弦值为
解法二:以 为坐标原点,射线
为坐标原点,射线 分别为
分别为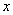 轴、
轴、 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系 . 设
. 设 ,则
,则 .
.
 的中点
的中点 ,
, .
.
 .
.
 故
故 等于二面角
等于二面角 的平面角.……10分
的平面角.……10分
 ,
,
所以二面角 的余弦值为
的余弦值为 .
.

练习册系列答案
相关题目
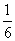 B.
B.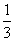 C.
C.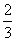 D.
D.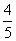
 =(-2,1),
=(-2,1), =(-2,-3),则
=(-2,-3),则 B. 0 C.
B. 0 C.  是( )
是( ) 的奇函数 B.周期为
的奇函数 B.周期为 的奇函数 D.周期为
的奇函数 D.周期为 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值是 ;
的最大值是 ; ,则
,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.

 ,若|
,若| |≥
|≥ ,则
,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 C.-
C.- D.-3
D.-3 的准线方程是
的准线方程是 ,则
,则 的值为( )
的值为( ) B.
B. C.8 D.
C.8 D.