题目内容
5．若函数f（x）是定义在R上的偶函数，在区间（-∞，0）上是减函数，则使f（lnx）＜f（1）的x的取值范围为（$\frac{1}{e}$，e）．分析 函数f（x）是R上的偶函数，且在（-∞，0]上是减函数，可得函数f（x）在[0，+∞）上是增函数，由f（lnx）＜f（1），即f（|lnx|）＜f（1），利用单调性即可得出．
解答 解：∵函数f（x）是R上的偶函数，且在（-∞，0]上是减函数，
∴函数f（x）在[0，+∞）上是增函数，
∵f（lnx）＜f（1），即f（|lnx|）＜f（1），
∴|lnx|＜1，∴-1＜lnx＜1，
解得：$\frac{1}{e}$＜x＜e
∴实数a的取值范围是（$\frac{1}{e}$，e），
故答案为：$（\frac{1}{e}，e）$．
点评 本题考查了函数的奇偶性、单调性，得到f（|lnx|）＜f（1）是解题的关键，属于中档题
练习册系列答案
阅读快车系列答案
相关题目
16．若$\overrightarrow a=（2x，1，3），\overrightarrow b=（1，-2y，9）$，若$\overrightarrow a$∥$\overrightarrow b$，则（ ）
| A． | x=1，y=1 | B． | $x=\frac{1}{2}，y=-\frac{1}{2}$ | C． | $x=\frac{1}{6}，y=-\frac{3}{2}$ | D． | $x=-\frac{1}{6}，y=\frac{3}{2}$ |
13．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1，F2，椭圆上存在点P，使得∠F1PF2=60°，则椭圆的离心率的取值范围是（ ）
| A． | $（{0，\frac{1}{2}}]$ | B． | $[{\frac{1}{2}，1}）$ | C． | $（{0，\frac{{\sqrt{3}}}{2}}]$ | D． | $[{\frac{{\sqrt{3}}}{2}，1}）$ |
20．已知0＜A＜$\frac{π}{2}$，且cosA=$\frac{2}{3}$，那么sin2A等于（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{7}{9}$ | C． | $\frac{8}{9}$ | D． | $\frac{{4\sqrt{5}}}{9}$ |
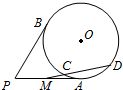如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=8，MC=2，则CD=6．