题目内容
已知命题p:?x∈R, .命题q:?x0∈R,
.命题q:?x0∈R, .若p或q为真,p且q为假,则m的取值范围
.若p或q为真,p且q为假,则m的取值范围
- A.m>1
- B.1<m≤3
- C.m>3
- D.m≤3
B
分析:先利用配方法求x2+x+ 的最小值,从而利用恒成立求得命题p的等价命题,再利用一元二次方程根的判别式,求得命题q的等价命题,最后利用真值表,判断两命题的真假,列不等式组即可即得m的范围
的最小值,从而利用恒成立求得命题p的等价命题,再利用一元二次方程根的判别式,求得命题q的等价命题,最后利用真值表,判断两命题的真假,列不等式组即可即得m的范围
解答:若命题p为真命题,则m小于或等于x2+x+ 的最小值,∵x2+x+
的最小值,∵x2+x+ =(x+
=(x+ )2+1≥1,∴m≤1
)2+1≥1,∴m≤1
若命题q为真命题,则方程的△=(-2m)2-4(m2+m-3)≥0,解得m≤3
∵p或q为真,p且q为假
∴p真q假,或p假q真
∴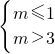 或
或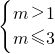
解得1<m≤3
故选 B
点评:本题主要考查了复合命题真假的判断,命题的真假与集合间的关系,二次函数的性质和二次方程的根的判别式的应用,全称命题与特称命题的真假判断
分析:先利用配方法求x2+x+
 的最小值,从而利用恒成立求得命题p的等价命题,再利用一元二次方程根的判别式,求得命题q的等价命题,最后利用真值表,判断两命题的真假,列不等式组即可即得m的范围
的最小值,从而利用恒成立求得命题p的等价命题,再利用一元二次方程根的判别式,求得命题q的等价命题,最后利用真值表,判断两命题的真假,列不等式组即可即得m的范围解答:若命题p为真命题,则m小于或等于x2+x+
 的最小值,∵x2+x+
的最小值,∵x2+x+ =(x+
=(x+ )2+1≥1,∴m≤1
)2+1≥1,∴m≤1若命题q为真命题,则方程的△=(-2m)2-4(m2+m-3)≥0,解得m≤3
∵p或q为真,p且q为假
∴p真q假,或p假q真
∴
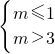 或
或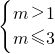
解得1<m≤3
故选 B
点评:本题主要考查了复合命题真假的判断,命题的真假与集合间的关系,二次函数的性质和二次方程的根的判别式的应用,全称命题与特称命题的真假判断

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目