��Ŀ����
17��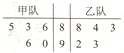 ij����������ǣ��Ƚ��и�������ÿ֧�����ӵijɼ�ǰ������Ա�ٴ������ӽ�������������������������������ͬ��Ա֮���������������ͬʱ���У�������������ͳ�ƣ�������Ա�и������ɼ��ߵĶ�Ա�ڸ�����ʤ�ĸ���Ϊ$\frac{2}{3}$�����ĸ���Ϊ$\frac{1}{3}$���Ҹ�����������Ӱ�죮��֪���ҶӸ�5����Ա����10����Ա�ĸ������ɼ���ͼ��ʾ��
ij����������ǣ��Ƚ��и�������ÿ֧�����ӵijɼ�ǰ������Ա�ٴ������ӽ�������������������������������ͬ��Ա֮���������������ͬʱ���У�������������ͳ�ƣ�������Ա�и������ɼ��ߵĶ�Ա�ڸ�����ʤ�ĸ���Ϊ$\frac{2}{3}$�����ĸ���Ϊ$\frac{1}{3}$���Ҹ�����������Ӱ�죮��֪���ҶӸ�5����Ա����10����Ա�ĸ������ɼ���ͼ��ʾ����I�����������ڸ������гɼ��ľ�ֵ�ͷ��
���������������������2����Ա��ʤ�ĸ��ʣ�
���� ������ƽ�����ͷ���Ĺ�ʽ���㼴�ɣ�
������������¼�ͬʱ�����ĸ��ʺͻ����¼��ĸ��ʵõ������
��� �⣺�����ɾ�Ҷͼ��֪��
$\overline{x��}$=$\frac{85+83+86+96+90}{5}$=88��$\overrightarrow{x��}$=$\frac{88+84+83+92+93}{5}$=88��
S${\;}_{��}^{2}$=$\frac{1}{5}$[��85-88��2+��83-88��2+��86-88��2+��96-88��2+��90-88��2]=21.2��
S${\;}_{��}^{2}$=$\frac{1}{5}$[��88-88��2+��84-88��2+��83-88��2+��92-88��2+��93-88��2]=16.4��
������ӲμӸ������������ɼ�ǰ�����ڶԿ����Ļ�ʤ���¼��ֱ�ΪA��B��C��
�������֪P��A��=$\frac{2}{3}$��P��B��=P��C��=$\frac{1}{3}$����A��B��C�������
�������2����Ա��ʤ���¼�ΪE����E=��ABC���ȣ�AB$\overline{C}$���ȣ�A$\overline{B}$C���ȣ�$\overline{A}$BC����
P��E��=$\frac{2}{3}$��$\frac{1}{3}$��$\frac{1}{3}$+$\frac{2}{3}$��$\frac{1}{3}$����1-$\frac{1}{3}$��+$\frac{2}{3}$����1-$\frac{1}{3}$����$\frac{1}{3}$+��1-$\frac{2}{3}$����$\frac{1}{3}$��$\frac{1}{3}$=$\frac{11}{27}$��
���� ���⾥Ҷͼ��ƽ��������������¼���������¼��ĸ��ʼ��㣬�����¼�һ���漰�������ۣ�ע��Ҫȫ��������������ز�©�������е��⣮

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�| A�� | $��\frac{1}{3}$ | B�� | ��$\frac{1}{2}$ | C�� | ��$\frac{\sqrt{3}}{2}$ | D�� | ��$\frac{\sqrt{2}}{2}$ |

| A�� | $\frac{4}{3}$����+1�� | B�� | $\frac{2}{3}$����+1�� | C�� | $\frac{4}{3}$����+$\frac{1}{2}$�� | D�� | $\frac{2}{3}$����+$\frac{1}{2}$�� |
| A�� | $-\frac{{3\sqrt{15}}}{2}$ | B�� | $\frac{{3\sqrt{15}}}{2}$ | C�� | $-\frac{{3\sqrt{2}}}{2}$ | D�� | $\frac{{3\sqrt{2}}}{2}$ |
 ��ͼ��������P-ABCD�У�AB��CD��PA��AD��CD��AD��PA=AD=CD=2AB��E��F�ֱ�ΪPC��CD���е㣬DE=EC��
��ͼ��������P-ABCD�У�AB��CD��PA��AD��CD��AD��PA=AD=CD=2AB��E��F�ֱ�ΪPC��CD���е㣬DE=EC��