题目内容
若函数f（x）=xlg
为偶函数，则a的值为（ ）
| a-x |
| x+1 |
| A、0 | B、-1 | C、1 | D、不存在 |
分析：因为函数f（x）=xlg
为偶函数，所以f（-x）=f（x），可得x（lg
）=0，所以a=±1．经检验当a=-1时，无意义，所以a=-1舍去，进而得到答案．
| a-x |
| x+1 |
| a2-x2 |
| 1-x2 |
解答：解：因为函数f（x）=xlg
为偶函数，
所以f（-x）=f（x），即-xlg（
）=xlg
，
整理可得：x[lg
+lg（
）]=0，即x（lg
）=0，
所以a=±1．
当a=-1时，
=-1无意义，所以a=-1舍去．
故选C．
| a-x |
| x+1 |
所以f（-x）=f（x），即-xlg（
| a+x |
| -x+1 |
| a-x |
| x+1 |
整理可得：x[lg
| a-x |
| x+1 |
| a+x |
| -x+1 |
| a2-x2 |
| 1-x2 |
所以a=±1．
当a=-1时，
| -1-x |
| x+1 |
故选C．
点评：本题主要考查函数的奇偶性，并且利用此性质求参数的数值，注意求参数后要验证结果．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
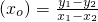，求证：xo＞xl．
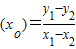，求证：xo＞xl．