题目内容

若不全为零的实数a，b，c成等差数列，点P（-1，-2）在动直线l：ax+by+c=0上的射影为M，点N（0，3），则线段MN长度的最小值是
 
．
分析：由于不全为零的实数a，b，c成等差数列，可得2b=a+c．代入直线l：ax+by+c=0可得a（2x+y）+c（y+2）=0．可得：动直线l过定点（1，-2）．由于PM⊥MQ，可知点M在以PQ为直径的圆上，进而得出答案．
解答：解：∵不全为零的实数a，b，c成等差数列，∴2b=a+c．把b=
a+c
2
代入直线l：ax+by+c=0可得ax+
a+c
2
y+c=0，
化为a（2x+y）+c（y+2）=0．
由于a，c不全为0，联立
2x+y=0
y+2=0
解得
x=1
y=-2
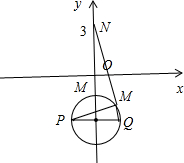
，精英家教网
可知：动直线l过定点Q（1，-2）．
设点M（x，y），∵PM⊥QM．
∴
PM
•
QM
=（x+1，y+2）•（x-1，y+2）=x2-1+（y+2）2=0，
化为x2+（y+2）2=1．
因此点M在以（0，-2）为圆心，1为半径的圆上，
故当取点M（0，-1）时，|MN|取得最小值3-（-1）=4．
故答案为：4．
点评：本题考查了等差数列的定义、直线系过定点问题、圆的标准方程及其性质、最小值问题等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
①
a
∥
b
?存在唯一的实数λ，使
b
=λ
a
；
②
a
∥
b
?存在不全为零的实数λ，μ，使λ
a
+μ
b
=
0
；
③
a
与
b
不共线?若存在实数λ，μ使λ
a
+μ
b
=
0
，则λ=μ=0；
④
a
与
b
不共线?不存在实数λ，μ使λ
a
+μ
b
=
0
．下列命题是真命题的是
 
（填序号）
已知a，b，c，d是不全为零的实数，函数f（x）=bx2+cx+d，g（x）=ax3+bx2+cx+d．方程f（x）=0有实数根，且f（x）=0的实数根都是g（f（x））=0的根；反之，g（f（x））=0的实数根都是f（x）=0的根．
（1）求d的值；
（2）若a=0，求c的取值范围；
（3）若a=1，f（1）=0，求c的取值范围．
设
a
、
b
为平面向量，若存在不全为零的实数λ，μ使得λ
a
+μ
b
=0，则称
a
、
b
线性相关，下面的命题中，
a
、
b
、
c
均为已知平面M上的向量．
①若
a
=2
b
，则
a
、
b
线性相关；
②若
a
、
b
为非零向量，且
a
⊥
b
，则
a
、
b
线性相关；
③若
a
、
b
线性相关，
b
、
c
线性相关，则
a
、
c
线性相关；
④向量
a
、
b
线性相关的充要条件是
a
、
b
共线．
上述命题中正确的是
 
（写出所有正确命题的编号）

设a、b为平面向量，若存在不全为零的实数使得，则除a、b线性相关，下面的命题中，a、b、c均为已知平面M上的向量。

       ①若a=2b，则a、b线性相关；

       ②若a、b为非零向量，且，则a、b线性相关；

       ③若a、b线性相关，b、c线性相关，则a、c线性相关；

       ④向量a、b线性相关的充要条件是a、b共线。

       上述命题中正确的是           （写出所有正确命题的编号）

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网