题目内容
已知函数f(x)=lnx-ax+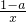 -1.
-1.
(1)当a=1时,求f(x)在(1,f(1))处的切线方程;
(2)当0<a≤ 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(3)设g(x)=x2-2bx+4,当a= 时,若对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,求实数b的取值范围.
时,若对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,求实数b的取值范围.
解:(1)当a=1时,f(x)=lnx-x-1,∴f′(x)=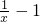
∴f′(1)=0
∵f(1)=-2
∴f(x)在(1,f(1))处的切线方程为y=-2;
(2)函数f(x)的定义域为(0,+∞),
求导函数,f′(x)=-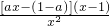
令f′(x)=0得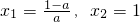
当a= 时,f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
时,f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
当0<a< 时,
时,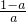 >1,
>1,
∴在(0,1)和(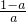 ,+∞)上,有f′(x)<0,函数f(x)单调递减,
,+∞)上,有f′(x)<0,函数f(x)单调递减,
在(1,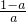 )上,f′(x)>0,函数f(x)单调递增;
)上,f′(x)>0,函数f(x)单调递增;
(3)当a= 时,
时,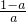 =3,f(x)=lnx-
=3,f(x)=lnx-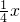 +
+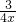 -1
-1
由(2)知,函数在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
有f(x1)≥f(1)=-
对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,
只需当x∈[1,2]时,[g(x)]max≤ 即可
即可
所以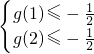 ,所以
,所以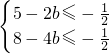
所以b≥
所以实数b的取值范围是[ ,+∞).
,+∞).
分析:(1)求导数,确定切线的斜率,从而可得f(x)在(1,f(1))处的切线方程;
(2)分类讨论.利用导数的正负,可得函数f(x)的单调性;
(3)确定f(x1)≥f(1)=- ,对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,只需当x∈[1,2]时,[g(x)]max≤
,对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,只需当x∈[1,2]时,[g(x)]max≤ 即可,由此可得不等式,从而可求实数b的取值范围.
即可,由此可得不等式,从而可求实数b的取值范围.
点评:本题考查导数的几何意义,考查利用导数研究函数的单调性,考查函数恒成立问题,属于中档题.
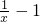
∴f′(1)=0
∵f(1)=-2
∴f(x)在(1,f(1))处的切线方程为y=-2;
(2)函数f(x)的定义域为(0,+∞),
求导函数,f′(x)=-
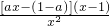
令f′(x)=0得
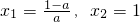
当a=
 时,f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
时,f′(x)≤0,函数f(x)在(0,+∞)上单调递减;当0<a<
 时,
时,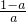 >1,
>1,∴在(0,1)和(
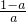 ,+∞)上,有f′(x)<0,函数f(x)单调递减,
,+∞)上,有f′(x)<0,函数f(x)单调递减,在(1,
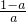 )上,f′(x)>0,函数f(x)单调递增;
)上,f′(x)>0,函数f(x)单调递增;(3)当a=
 时,
时,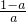 =3,f(x)=lnx-
=3,f(x)=lnx-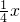 +
+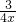 -1
-1由(2)知,函数在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
有f(x1)≥f(1)=-

对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,
只需当x∈[1,2]时,[g(x)]max≤
 即可
即可所以
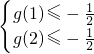 ,所以
,所以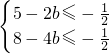
所以b≥

所以实数b的取值范围是[
 ,+∞).
,+∞).分析:(1)求导数,确定切线的斜率,从而可得f(x)在(1,f(1))处的切线方程;
(2)分类讨论.利用导数的正负,可得函数f(x)的单调性;
(3)确定f(x1)≥f(1)=-
 ,对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,只需当x∈[1,2]时,[g(x)]max≤
,对任意x1∈(0,2),当x2∈[1,2]时,f(x1)≥g(x2)恒成立,只需当x∈[1,2]时,[g(x)]max≤ 即可,由此可得不等式,从而可求实数b的取值范围.
即可,由此可得不等式,从而可求实数b的取值范围.点评:本题考查导数的几何意义,考查利用导数研究函数的单调性,考查函数恒成立问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目