题目内容
设函数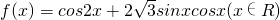
的最大值为M，最小正周期为T．
（1）求M、T；
（2）求f（x）的单调递减区间．
解：（1）
=2（sin
cos2x+cossin2x）=
∴M=2，T=
=π
（2）当
，即
时，f（x）单调递减．
∴f（x）的单调递减区间为
．
分析：（1）利用二倍角公式和两角和的正弦公式将已知函数解析式化为y=Asin（ωx+φ）型函数，再利用三角函数的图象和性质计算最值和周期即可；
（2）将内层函数置于外层函数的减区间上，解不等式即可得函数的单调递减区间
点评：本题考查了二倍角公式和两角和的正弦公式的运用，y=Asin（ωx+φ）型函数的图象和性质，复合函数单调区间的求法，属中档题
=2（sincos2x+cossin2x）=∴M=2，T=
=π（2）当
，即时，f（x）单调递减．∴f（x）的单调递减区间为
．分析：（1）利用二倍角公式和两角和的正弦公式将已知函数解析式化为y=Asin（ωx+φ）型函数，再利用三角函数的图象和性质计算最值和周期即可；
（2）将内层函数置于外层函数的减区间上，解不等式即可得函数的单调递减区间
点评：本题考查了二倍角公式和两角和的正弦公式的运用，y=Asin（ωx+φ）型函数的图象和性质，复合函数单调区间的求法，属中档题
练习册系列答案
相关题目
的最大值为M，
满足
M，且
（i=1,2,…10）求
…
的值.
的最大值为M，最小正周期为T.
满足
求
的值.
的最大值为M，最小正周期为T．
的最大值为M，最小值为N,那么M＋N＝＿＿＿＿＿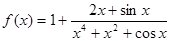
的最大值为M，最小值为m，则M+m的值为( )