题目内容
已知等比数列{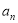 }的前
}的前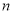 项和为
项和为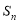 ,且满足
,且满足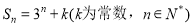 .
.
(1)求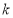 的值及数列{
的值及数列{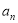 }的通项公式;
}的通项公式;
(2)若数列{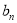 }满足
}满足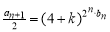 ,求数列{
,求数列{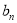 }的前
}的前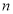 和
和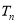 .
.
(1)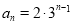 (2)
(2)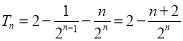
【解析】
试题分析:(1)通过前n项和公式,列出关于关于前3项的方程组,可求得,然后利用等比中项求出k,可求得通项公式.
(2)首先求出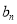 的通项公式,然后作差,结果利用等比数列求和,可求得.
的通项公式,然后作差,结果利用等比数列求和,可求得.
试题解析:【解析】
(1)方法一
由题意,有 1分
1分
∴ 2分
2分
又∵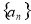 为等比数列,∴
为等比数列,∴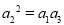 ,即
,即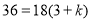 ,解得
,解得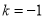 , 4分
, 4分
∴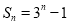 .
.
当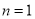 时,
时,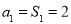 , 5分
, 5分
当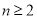 时,
时,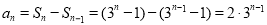 , 6分
, 6分
显然,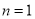 时也适合
时也适合 ,
,
∴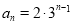 . 7分
. 7分
方法二
当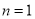 时,
时, ; 1分
; 1分
当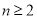 时,
时,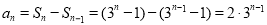 . 3分
. 3分
∵数列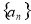 是等比数列,∴
是等比数列,∴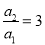 , 4分
, 4分
即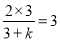 , 5分
, 5分
解得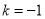 , 6分
, 6分
∴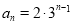 . 7分
. 7分
(2)将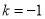 及
及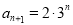 ,代入
,代入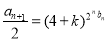 ,得
,得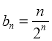 , 9分
, 9分
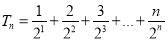 ①
①
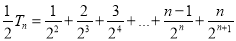 ② 11分
② 11分
①-②得: 12分
12分
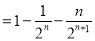 13分
13分
∴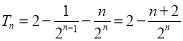 . 14分
. 14分
考点:数列的求和,等比数列的通项公式
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (n∈N*)均在函数
(n∈N*)均在函数 的图象上,则a2014=( )
的图象上,则a2014=( ) 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值
的最小值 D.4
D.4 上,有两个不同的实数值满足方程
上,有两个不同的实数值满足方程 =
= ,则
,则 的取值范围是( )
的取值范围是( ) B、
B、 C、
C、 D、
D、
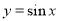 B、
B、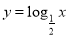 C、
C、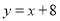 D、
D、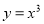
 ”的否定是( )
”的否定是( )



 ,则目标函数
,则目标函数 的最小值是
的最小值是  有两个零点,则
有两个零点,则 应满足的充要条件是 .
应满足的充要条件是 .