Question

在平行四边形ABCD中，∠BAD＝60°，AD＝2AB，若P是平面ABCD内一点，且满足：x＋y＋＝0(x，y∈R)．则当点P在以A为圆心，||为半径的圆上时，实数x，y应满足关系式为          (　　)．

A．4x²＋y²＋2xy＝1           B．4x²＋y²－2xy＝1

C．x²＋4y²－2xy＝1           D．x²＋4y²＋2xy＝1

Answer 1

D

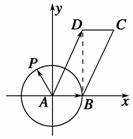
解析　如图，以A为原点建立平面直角坐标系，设AD＝2.据题意，得AB＝1，∠ABD＝90°，BD＝.∴B、D的坐标分别为(1,0)、(1，)，∴＝(1,0)，＝(1，)．设点P的坐标为(m，n)，即＝(m，n)，则由x＋y＋＝0，得：＝x＋y，∴

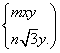
据题意，m²＋n²＝1，∴x²＋4y²＋2xy＝1.