题目内容
设定义在R上的函数 (a0,a1,a2,a3∈R),当x=-1时,f(x)取极大值
(a0,a1,a2,a3∈R),当x=-1时,f(x)取极大值 ,且函数y=f(x)的图象关于点(0,0)对称.
,且函数y=f(x)的图象关于点(0,0)对称.
(Ⅰ)求f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在 上;
上;
(Ⅲ)设 ,
, ,求证:
,求证: .
.
(Ⅰ)解:由f(x)的图象关于点(0,0)对称,即f(x)是奇函数,所以 .
.
由题意当x=-1时,f(x)取极大值 ,得
,得 ,所以
,所以 ,
,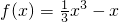 .
.
所以,所求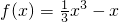 .…(4分)
.…(4分)
( II)解:f'(x)=x2-1.设所求两点为(x1,f(x1)),(x2,f(x2)),x1,x2∈[ ,得
,得
因为 ,所以
,所以 或
或
即x1=0,x2=± 或x1=
或x1= ,x2=0
,x2=0
从而可得所求两点的坐标为:(0,0), 或者(0,0),
或者(0,0), .…(8分)
.…(8分)
(III)证明: ,当
,当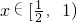 时,f'(x)<0,即在
时,f'(x)<0,即在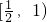 上递减,得
上递减,得 ,即
,即 .
.
∵ ,由导数可得
,由导数可得 ,即
,即 ,
,
所以 …(12分)
…(12分)
分析:(Ⅰ)由f(x)的图象关于点(0,0)对称,即f(x)是奇函数,可得 ,根据当x=-1时,f(x)取极大值
,根据当x=-1时,f(x)取极大值 ,建立方程组,即可求得函数的不等式;
,建立方程组,即可求得函数的不等式;
( II)设所求两点为(x1,f(x1)),(x2,f(x2)),x1,x2∈[ ,利用两点为切点的切线互相垂直即可求得点的坐标;
,利用两点为切点的切线互相垂直即可求得点的坐标;
(III)确定f(ym)的最大值,f(xn)的最小值,即可证得结论.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的最值,考查不等式的证明,正确求导,确定函数的最值是关键.
 .
.由题意当x=-1时,f(x)取极大值
 ,得
,得 ,所以
,所以 ,
,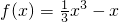 .
.所以,所求
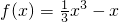 .…(4分)
.…(4分)( II)解:f'(x)=x2-1.设所求两点为(x1,f(x1)),(x2,f(x2)),x1,x2∈[
 ,得
,得
因为
 ,所以
,所以 或
或
即x1=0,x2=±
 或x1=
或x1= ,x2=0
,x2=0从而可得所求两点的坐标为:(0,0),
 或者(0,0),
或者(0,0), .…(8分)
.…(8分)(III)证明:
 ,当
,当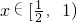 时,f'(x)<0,即在
时,f'(x)<0,即在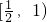 上递减,得
上递减,得 ,即
,即 .
.∵
 ,由导数可得
,由导数可得 ,即
,即 ,
,所以
 …(12分)
…(12分)分析:(Ⅰ)由f(x)的图象关于点(0,0)对称,即f(x)是奇函数,可得
 ,根据当x=-1时,f(x)取极大值
,根据当x=-1时,f(x)取极大值 ,建立方程组,即可求得函数的不等式;
,建立方程组,即可求得函数的不等式;( II)设所求两点为(x1,f(x1)),(x2,f(x2)),x1,x2∈[
 ,利用两点为切点的切线互相垂直即可求得点的坐标;
,利用两点为切点的切线互相垂直即可求得点的坐标;(III)确定f(ym)的最大值,f(xn)的最小值,即可证得结论.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的最值,考查不等式的证明,正确求导,确定函数的最值是关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |