题目内容
11.已知矩阵A=$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$(1)矩阵A=$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$对应的变换把直线l:x+y=0变为直线l′,求直线l′的方程.
(2)求A的逆矩阵A-1.
分析 (1)任取直线l:x+y=0上一点P(x′,y′),经矩阵变换后点为P(x′,y),利用矩阵乘法得出坐标之间的关系,求出直线l′的方程;
(2)求出|A|,即可求A的逆矩阵A-1.
解答 解:(1)任取直线l:x+y=0上一点P(x′,y′),
经矩阵变换后点为P′(x,y),则有$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$(x′,y′)=(x,y),
可得$\left\{\begin{array}{l}{x=x′+2y′}\\{y=-x′+2y′}\end{array}\right.$,解得$\left\{\begin{array}{l}{x′=\frac{x-y}{2}}\\{y′=\frac{x+y}{4}}\end{array}\right.$,
代入直线l:x′+y′=0,化简得3x-y=0.
直线l′的方程3x-y=0;
(2)∵矩阵A=$(\begin{array}{l}{1}&{2}\\{-1}&{2}\end{array})$,
∴|A|=1×2-2×(-1)=4,
∴A-1=$[\begin{array}{l}{\frac{1}{2}}&{-\frac{1}{2}}\\{\frac{1}{4}}&{\frac{1}{4}}\end{array}]$.
点评 本题以矩阵为依托,考查矩阵的乘法,矩阵,考查矩阵变换,关键是正确利用矩阵的乘法公式.

练习册系列答案
相关题目
15.平面α上存在不同的三点到平面β的距离相等且不为零,则平面α与平面β的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或重合 | D. | 平行或相交 |
13.向量$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(2,4),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$,$\overrightarrow{d}$=λ$\overrightarrow{a}$-$\overrightarrow{b}$,若$\overrightarrow{c}$⊥$\overrightarrow{d}$,则λ的值为( )
| A. | $\frac{1±5\sqrt{2}}{7}$ | B. | $\frac{5±\sqrt{221}}{14}$ | C. | ±1 | D. | 以上A、B、C均不对 |
6.已知椭圆的左焦点为F1,右焦点为F2.若椭圆上存在一点P,满足线段PF2相切于以椭圆的短轴为直径的圆,切点为线段PF2的中点,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
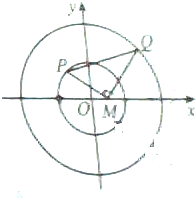 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.