Question

已知函数f（x）=

1

3

x³-

m+1

2

x²（x∈R）．
（1）若f（x）在x=1处取得极大值，求函数f（x）的单调区间；
（2）若关于x的方程f（x）=

1

3

-mx（m≤1）有三个不同的根，求实数m的取值范围．

Answer 1

（1）f′（x）=x²-（m+1）x，…（1分）
则由题意，f（x）在x=1处取得极大值
∴f′（1）=1²-（m+1）×1=0，即m=0．…（2分）
∴f（x）=

1

3

x³-

1

2

x²，f′（x）=x²-x．
由f′（x）=x²-x=0，解得x=0或x=1．
令f′（x）＞0，得x＜0或x＞1；令f′（x）＜0，得0＜x＜1．
∴函数f（x）的单调递增区间是（-∞，0）和（1，+∞），单调递减区间是（0，1）．…（5分）
（2）设g（x）=f（x）+mx-

1

3

=

1

3

x³-

m+1

2

x²+mx-

1

3

，
则g′（x）=x²-（m+1）x+m=（x-m）（x-1）．
令g′（x）=0，得x=m或x=1．
①当m=1时，g′（x）=（x-1）²≥0，g（x）在R上单调递增，不合题意．…（7分）


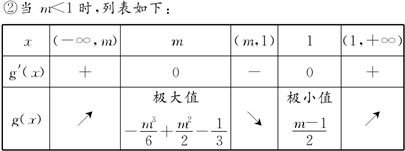
  …（9分）
因为方程f（x）=

1

3

-mx（m≤1）有三个不同的根，即函数g（x）=f（x）+mx-

1

3

与x轴有三个不同的交点，所以

- m3 6 + m2 2 - 1 3 ＞0 m-1 2 ＜0

            …（10分）
解得m＜1-

3

．…（12分）
综上所述，实数m的取值范围是（-∞，1-

3

）．  …（13分）