题目内容
21.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
![]() (cos
(cos ![]() =
=![]() )方向
)方向
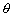
21.解法一:设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60(km).
若在时刻t城市O受到台风的侵袭,则OQ≤10t+60.
由余弦定理知OQ2=PQ2+PO2-2·PQ·POcosOPQ.
由于 PO=300,PQ=20t,
cosOPQ=cos(![]() -45°)
-45°)
=cos![]() cos45°+sin
cos45°+sin![]() sin45°
sin45°
=![]() ×
×![]() +
+![]() ×
×![]()
=![]() ,
,
故 OQ2=(20t)2+3002-2×20t×300×![]()
=202t2-9600t+3002.
因此 202t2-9600t+3002≤(10t+60)2,
即 t2-36t+288≤0,
解得 12≤t≤24.
答:12小时后该城市开始受到台风的侵袭.
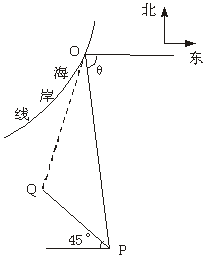
解法二:如图建立坐标系:以O为原点,正东方向为x轴正向.
在时刻t(h)台风中心![]() 的坐标为
的坐标为
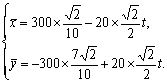
此时台风侵袭的区域是(x-![]() )2+(y-
)2+(y-![]() )2≤[r(t)]2,
)2≤[r(t)]2,
其中r(t)=10t+60.
若在t时刻城市O受到台风的侵袭,则有(0-![]() )2+(0-
)2+(0-![]() )2≤(10t+60)2,
)2≤(10t+60)2,
即 (300×![]() -20×
-20×![]() t)2+(-300×
t)2+(-300×![]() +20×
+20×![]() t)2≤(10t+60)2,
t)2≤(10t+60)2,
即 t2-36t+288≤0,
解得 12≤t≤24.
答:12小时后该城市开始受到台风的侵袭.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案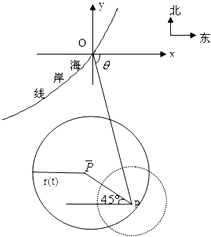 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 

 方向300 km的海面P处,并以20 km
/ h的速度向西偏北
方向300 km的海面P处,并以20 km
/ h的速度向西偏北 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭?持续多长时间?