题目内容
已知函数 ,
, ,若对于任一实数
,若对于任一实数 ,
, 与
与 至少有一个为正数,则实数
至少有一个为正数,则实数 的取值范围是
的取值范围是
 ,
, ,若对于任一实数
,若对于任一实数 ,
, 与
与 至少有一个为正数,则实数
至少有一个为正数,则实数 的取值范围是
的取值范围是A. | B. | C. | D. |
B
试题分析:当m≤0时,显然不成立,当m=0时,因f(0)=1>0,
当m>0时,若 ,即
,即 时结论显然成立;
时结论显然成立;
若 时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8,
时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8,
则0<m<8,故选B.
点评:解本小题的突破口是因为g(x)=mx显然对任一实数x不可能恒为正数,所以应按 和
和 分类研究,g(x)的取值,进而判断出f(x)的取值,从而找到解决此问题的途径.
分类研究,g(x)的取值,进而判断出f(x)的取值,从而找到解决此问题的途径.
当m>0时,若
 ,即
,即 时结论显然成立;
时结论显然成立;若
 时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8,
时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8,则0<m<8,故选B.
点评:解本小题的突破口是因为g(x)=mx显然对任一实数x不可能恒为正数,所以应按
 和
和 分类研究,g(x)的取值,进而判断出f(x)的取值,从而找到解决此问题的途径.
分类研究,g(x)的取值,进而判断出f(x)的取值,从而找到解决此问题的途径.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
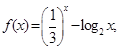 实数
实数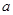 、
、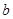 、
、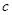 满足
满足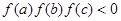 ,(0<
,(0<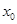 是函数
是函数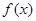 的一个零点,那么下列不等式中,不可能成立的是 ( )
的一个零点,那么下列不等式中,不可能成立的是 ( )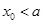
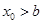
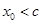
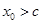
 的零点的个数是( )
的零点的个数是( )
 有负根,则a的取值范围是____________
有负根,则a的取值范围是____________ ,则方程
,则方程 在下面哪个区间内必有实根( )
在下面哪个区间内必有实根( )



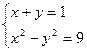 的解集是_____________.
的解集是_____________.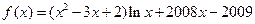 ,则方程
,则方程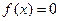 在下面哪个范围内必有实根( )
在下面哪个范围内必有实根( )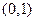
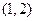
 有两个零点,则
有两个零点,则 的取值范围是
的取值范围是


