题目内容

2．在△ABC中，若$cosA=\frac{sinB}{sinC}$，则△ABC的形状为（　　）
A．锐角三角形B．直角三角形C．等腰三角形D．钝角三角形

分析 利用两角和公式对原等式整理求得cosA的值，判断出三角形的形状．

解答 解：整理原等式得sinCcosA=sin（A+C）=sinAcosC+cosAsinC，
∴sinCcosA=0，
∵sinC≠0，
∴cosA=0，A=$\frac{π}{2}$，
∴三角形为直角三角形，
故选B．

点评 本题主要考查了两角和公式的运用．属于基础题．

练习册系列答案
相关题目
12．已知点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上，F1，F2是这条双曲线上的两个焦点，$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0，且△F1PF2的三条边的长度成等差数列，则此双曲线的离心率的值为5．
13．已知函数f（x）=x3+ax2+bx+c的图象经过原点，且在x=1处取得极大值．
（Ⅰ）求实数a的取值范围；
（Ⅱ）若方程f（x）=-$\frac{{{{（{2a+3}）}^2}}}{9}$恰好有两个不同的根，求f（x）的解析式；
（Ⅲ）对于（2）中的函数f（x），若对于任意实数α和β恒有不等式|f（2sinα）-f（2sinβ）|≤m成立，求m的最小值．
10．已知角α的终边上一点P落在直线y=2x上，则sin2α=（　　）
A．$-\frac{{2\sqrt{5}}}{5}$B．$\frac{{2\sqrt{5}}}{5}$C．$-\frac{4}{5}$D．$\frac{4}{5}$
17．已知函数f（x）=x2+ax+b满足f（-1）=-2，且对于任意x∈R，恒有f（x）≥2x成立．
（1）求实数a，b的值；
（2）关于x的不等式f（x）＞2x|x-t|
①若t=1，求上述不等式的解集；
②若上述不等式对任意x∈[$\frac{1}{2}$，2]恒成立，求实数t的取值范围．
7．某算法的程序框图如图所示，若输入量S=1，a=5，则输出S=20．（考点：程序框图）
14．直线l的参数方程是$\left\{\begin{array}{l}x=1+2t\\ y=2-t\end{array}\right.\;\;（t∈R）$，则l的方向向量$\overrightarrow d$可以是$（{1，-\frac{1}{2}}）$或（-2，1）．
11．在数列{an}中，已知a1=-1，an+an+1+4n+2=0．
（1）若bn=an+2n．求证：{bn}是等比数列，并写出{bn}的通项公式．
（2）求{an}的通项公式及前n项和Sn．
12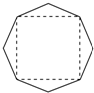．某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（　　）
A．2sin α-2cos α+2B．sin α-$\sqrt{3}$cos α+3C．3sin α-$\sqrt{3}$cos α+1D．2sin α-cos α+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网