题目内容
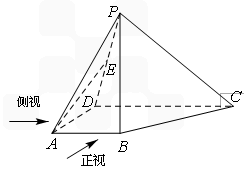
如图,在四棱锥P-ABCD中,PB⊥平面ABCD,AB⊥AD,AB∥CD,且AB=1,AD=CD=2,E在线段PD上.
(Ⅰ)若E是PD的中点,试证明: AE∥平面PBC;
(Ⅱ)若异面直线BC与PD所成的角为60°,求四棱锥P-ABCD的侧视图的面积.
(Ⅰ)若E是PD的中点,试证明: AE∥平面PBC;
(Ⅱ)若异面直线BC与PD所成的角为60°,求四棱锥P-ABCD的侧视图的面积.
解:(Ⅰ)解法一:在四棱锥P-ABCD中,取PC的中点F,连结EF、FB,
因为E是PD的中点,所以EF
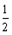 CD
CD AB,
AB,
所以四边形AEFB是平行四边形,
则AE∥FB,
而AE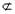 平面PBC,FB
平面PBC,FB 平面PBC,
平面PBC,
∴AE∥平面PBC.

解法二:如图,以B为坐标原点,AB所在直线为x轴,垂直于AB的直线为y轴,
BP所在直线为z轴,建立空间直角坐标系,
设PB=t, 则P(0,0,t),D(-1,2,0),C(1,2,0),A(-1,0,0),
所以E(-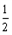 ,1,
,1,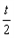 ),
),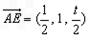 ,
,
设平面PBC的法向量为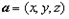 ,则
,则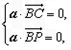
所以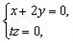 即
即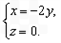
取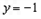 ,得到平面PBC的法向量为
,得到平面PBC的法向量为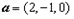 .
.
所以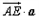 =0,而AE
=0,而AE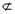 平面PBC,则AE∥平面PBC.
平面PBC,则AE∥平面PBC.
(Ⅱ)同(Ⅰ)法二建立空间直角坐标系,
设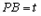 (t>0),则P(0,0,t),D(-1,2,0),C(1,2,0),
(t>0),则P(0,0,t),D(-1,2,0),C(1,2,0),
所以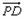 =(-1,2,-t),
=(-1,2,-t),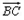 =(1,2,0),
=(1,2,0),
则|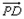 |=
|=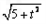 ,|
,|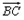 |=
|=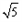 ,
,
由已知异面直线BC与PD成60°角,
所以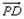 ·
·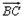 =
=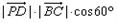 =
=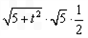 ,
,
又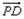 ·
·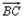 ==-1×1+2×2+(-t)×0=3,
==-1×1+2×2+(-t)×0=3,
所以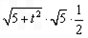 =3,解得t=
=3,解得t=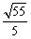 ,即PB=
,即PB=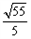 ,
,
所以侧视图的面积为S=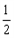 ×2×
×2×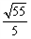 =
=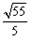
因为E是PD的中点,所以EF

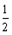 CD
CD AB,
AB, 所以四边形AEFB是平行四边形,
则AE∥FB,
而AE
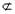 平面PBC,FB
平面PBC,FB 平面PBC,
平面PBC,∴AE∥平面PBC.

解法二:如图,以B为坐标原点,AB所在直线为x轴,垂直于AB的直线为y轴,
BP所在直线为z轴,建立空间直角坐标系,
设PB=t, 则P(0,0,t),D(-1,2,0),C(1,2,0),A(-1,0,0),
所以E(-
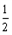 ,1,
,1,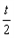 ),
),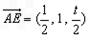 ,
,设平面PBC的法向量为
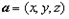 ,则
,则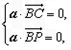
所以
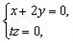 即
即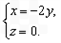
取
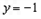 ,得到平面PBC的法向量为
,得到平面PBC的法向量为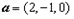 .
.所以
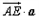 =0,而AE
=0,而AE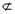 平面PBC,则AE∥平面PBC.
平面PBC,则AE∥平面PBC.(Ⅱ)同(Ⅰ)法二建立空间直角坐标系,
设
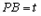 (t>0),则P(0,0,t),D(-1,2,0),C(1,2,0),
(t>0),则P(0,0,t),D(-1,2,0),C(1,2,0),所以
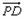 =(-1,2,-t),
=(-1,2,-t),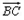 =(1,2,0),
=(1,2,0),则|
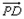 |=
|=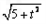 ,|
,|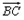 |=
|=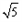 ,
, 由已知异面直线BC与PD成60°角,
所以
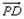 ·
·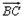 =
=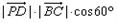 =
=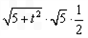 ,
,又
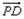 ·
·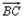 ==-1×1+2×2+(-t)×0=3,
==-1×1+2×2+(-t)×0=3, 所以
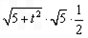 =3,解得t=
=3,解得t=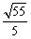 ,即PB=
,即PB=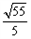 ,
,所以侧视图的面积为S=
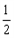 ×2×
×2×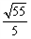 =
=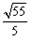

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
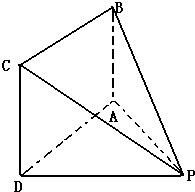 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且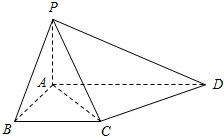 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=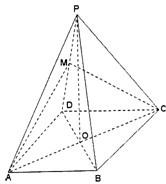 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.