Question

已知函数f（x）=ax³+bx²+cx的图象如右图所示，则关于a、b、c的符号分别是________．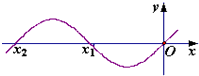

Answer 1

a＞0，b＞0，c＞0
分析：利用函数的通项得到函数的单调性情况，据函数的单调性与导函数的符号的关系得到导函数的符号情况，于是得到a的符号；根据函数的图象，判断出函数的零点情况，利用韦达定理求出b，c的符号．
解答：据函数f（x）的图象得到f（x）的单调性：f（x）先增再减再增
所以先f′（x）＞0再f′（x）＜0再f′（x）＞0
∵f′（x）=3ax²+2bx+c
∴a＞0
∵据函数f（x）的图象得到f（x）的三个零点一个为0，另两个为负
f（x）=ax³+bx²+cx=x（ax²+2bx+c）
∴
∴b＞0，c＞0
故答案为a＞0，b＞0，c＞0
点评：解决函数的单调性问题，一般利用导函数的符号与单调性的关系，函数递增对应导函数大于0求出的自变量的范围；函数递减对应导函数小于0求出的自变量的范围．