题目内容
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,且当
的奇函数,且当![]() 时,
时,![]() ,其中
,其中![]() 是常数.
是常数.
(1)求![]() 的解析式;
的解析式;
(2)求实数![]() 的值,使得函数
的值,使得函数![]() ,
,![]() 的最小值为
的最小值为![]() ;
;
(3)已知函数![]() 满足:对任何不小于
满足:对任何不小于![]() 的实数
的实数![]() ,都有
,都有![]() ,其中
,其中![]() 为不小于
为不小于![]() 的正整数常数,求证:
的正整数常数,求证:![]() .
.
【答案】(1)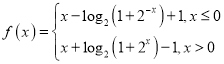 ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由函数![]() 是
是![]() 上的奇函数得出
上的奇函数得出![]() ,可解出
,可解出![]() ,再令
,再令![]() ,求出
,求出![]() ,利用奇函数的定义得出
,利用奇函数的定义得出![]() 的表达式,从而得出函数
的表达式,从而得出函数![]() 在
在![]() 上的解析式;
上的解析式;
(2)由题意得出![]() ,令
,令![]() ,可得出
,可得出![]() ,再分
,再分![]() 、
、![]() 、
、![]() 三种情况讨论,分析该二次函数在区间
三种情况讨论,分析该二次函数在区间![]() 上的单调性,得出该二次函数的最小值为
上的单调性,得出该二次函数的最小值为![]() ,求出
,求出![]() 的值;
的值;
(3)先求出![]() ,任取
,任取![]() 且
且![]() ,利用作差法证明出
,利用作差法证明出![]() ,由此得出
,由此得出![]() ,
,![]() ,
,![]() ,
,![]() ,再利用同向不等式的可加性可得出所证不等式成立.
,再利用同向不等式的可加性可得出所证不等式成立.
(1)由于函数![]() 是
是![]() 上的奇函数,则
上的奇函数,则![]() ,
,
那么,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
![]() .
.![]() 也适合
也适合![]() .
.
因此,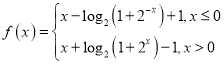 ;
;
(2)当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,
,
该二次函数图象开口向上,对称轴为直线![]() .
.
①当![]() 时,即当
时,即当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,此时,
上单调递增,此时,![]() ,解得
,解得![]() ,合乎题意;
,合乎题意;
②当![]() 时,即当
时,即当![]() 时,函数
时,函数![]() 在
在![]() 上取得最小值,即
上取得最小值,即![]() ,整理得
,整理得![]() ,解得
,解得![]() ,
,
均不符合题意;
③当![]() 时,即当
时,即当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
此时,![]() ,不合乎题意.
,不合乎题意.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ;
;
(3)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,则
,则![]() ,
,
整理得![]() ,解得
,解得![]() .
.
任取![]() 且
且![]() ,
,
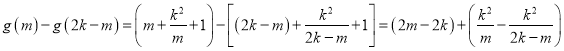
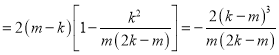 ,
,
![]() 且
且![]() ,
,![]() ,
,![]() ,所以,
,所以,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
上述不等式全部相加得![]() .
.

【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟).
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 34 | 51 | 59 | 66 | 65 | 25 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 40 | 160 | |
合计 |
(2)通过计算判断,是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关?
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |