题目内容
已知函数y=(1)求实数m的取值范围;
(2)当m变化时,若y的最小值为f(m),求函数f(m)的解析式.
思路解析:在求m的取值范围时,由于m为二次项系数∴要对其进行分类讨论;在求y的最小值时,可以用配方法,也可以用求二次函数的最值公式ymax(或ymin)=![]() .
.
解:(1)依题意,当x∈R时,mx2-6mx+m+8≥0恒成立.
当m=0,x∈R;当m≠0时,![]() 即
即
解之得0<m≤1,故0≤m≤1.
(2)当m=0时,y=2![]() ;
;
当0<m≤1时,y=![]() ,
,
∴ymin=![]() ,
,
因此f(m)= ![]() (0≤m≤1).
(0≤m≤1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域是A,函数y=
的定义域是A,函数y=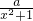 (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.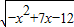 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.