题目内容
下列函数中,在其定义域上为奇函数的是( )
分析:根据函数奇偶性的定义逐项判断即可.
解答:解:f(x)=2x为非奇非偶函数;
f(x)=log2x定义域为(0,+∞),不关于原点对称,为非奇非偶函数;
f(x)=x2为偶函数;
f(x)=tan2x的定义域为{x|x≠
+
,k∈Z},关于原点对称,
且f(-x)=tan(-2x)=-tan2x=-f(x),
所以f(x)=tan2x为奇函数.
故选A.
f(x)=log2x定义域为(0,+∞),不关于原点对称,为非奇非偶函数;
f(x)=x2为偶函数;
f(x)=tan2x的定义域为{x|x≠
| kπ |
| 2 |
| π |
| 4 |
且f(-x)=tan(-2x)=-tan2x=-f(x),
所以f(x)=tan2x为奇函数.
故选A.
点评:本题考查函数奇偶性的判断,属基础题,定义是解决该类问题的基本方法.

练习册系列答案
相关题目
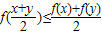 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数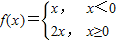
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数