题目内容
设集合A={(x,y)||x|+|y|≤1},B={(x,y)|(y-x)(y+x)≤0},M=A∩B,若动点P(x,y)∈M,则x2+(y-1)2的取值范围是
- A.
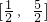
- B.
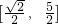
- C.
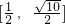
- D.
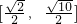
A
分析:集合A={(x,y)||x|+|y|≤1},B={(x,y)|(y-x)(y+x)≤0},M=A∩B,可以画出其可行域,目标函数z=x2+(y-1)2表示可行域中的点到圆心(0,1)距离的平方,从而进而求解;
解答:集合A={(x,y)||x|+|y|≤1},
B={(x,y)|(y-x)(y+x)≤0},可以若x>0,-x≤y≤x;若x<0可得,x≤y≤-x
M=A∩B,
可以画出可行域M:

目标函数z=x2+(y-1)2表示可行域中的点到圆心(0,1)距离的平方,
由上图可知:z在点A或C可以取得最小值,即圆心(0,1)到直线y=x的距离的平方,
zmin=d2=( )2=
)2= ,
,
z在点B或D处取得最大值,zmax=|0B|2=( )2+(
)2+( )2=
)2= ,
,
∴ ≤z≤
≤z≤ ,
,
故选A;
点评:此题主要考查线性规划的应用,解决此题的关键是画出可行域,考查的知识点比较全面,是一道基础题;
分析:集合A={(x,y)||x|+|y|≤1},B={(x,y)|(y-x)(y+x)≤0},M=A∩B,可以画出其可行域,目标函数z=x2+(y-1)2表示可行域中的点到圆心(0,1)距离的平方,从而进而求解;
解答:集合A={(x,y)||x|+|y|≤1},
B={(x,y)|(y-x)(y+x)≤0},可以若x>0,-x≤y≤x;若x<0可得,x≤y≤-x
M=A∩B,
可以画出可行域M:

目标函数z=x2+(y-1)2表示可行域中的点到圆心(0,1)距离的平方,
由上图可知:z在点A或C可以取得最小值,即圆心(0,1)到直线y=x的距离的平方,
zmin=d2=(
 )2=
)2= ,
,z在点B或D处取得最大值,zmax=|0B|2=(
 )2+(
)2+( )2=
)2= ,
,∴
 ≤z≤
≤z≤ ,
,故选A;
点评:此题主要考查线性规划的应用,解决此题的关键是画出可行域,考查的知识点比较全面,是一道基础题;

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为( )
| A、(1,3) | ||||
| B、(1,1) | ||||
C、(
| ||||
D、(
|



