题目内容

在△OAB中，
OA
=
a
，
OB
=
b
，OD是AB边上的高，若
AD
=λ
AB
则λ等于（　　）
A．
a
•(
b
-
a
)
|
a
-
b
|2
B．
a
(
b
-
a
)
|
a
-
b
|2
C．
a
(
b
-
a
)
|
a
-
b
|
D．
a
(
b
-
a
)
|
a
-
b
|
∵
AB
=
b
-
a

∴
AD
 =λ(
b
-
a
)
∴
OD
=
OA
+
AD
=
a
+λ(
b
-
a
)
∴
AD
⊥
OD

∴∴
AD
•
OD
=0
∴[
a
+λ(
b
-
a
)]•λ(
b
-
a
)=0
解得λ=
a
(
b
-
a
)
|
a
-
b
|2

故选B．
练习册系列答案
相关题目
在△OAB中，
OA
=
a
，
OB
=
b
，M为OB的中点，N为AB的中点，ON，AM交于点P，则
AP
=（　　）
A、
2
3
a
-
1
3
b
B、-
2
3
a
+
1
3
b
C、
1
3
a
-
2
3
b
D、-
1
3
a
+
2
3
b
如图所示，在△OAB中，OA＞OB，OC=OB，设
OA
=
a
，
OB
=
b
，若
AC
=λ•
AB
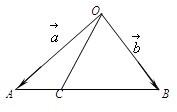
，则实数λ的值为（　　）精英家教网
A、
a
•(
a
-
b
)  
|
a
-
b
|
B、
a
•(
a
-
b
)  
|
a
-
b
|2
C、
a
2-
b
2
|
a
-
b
|
D、
a
2-
b
2
|
a
-
b
|2
在△OAB中，
OA
=
a
，
OB
=
b
，M为OB的中点，N为AB的中点，ON，AM交于点P，则
AP
=
 
．
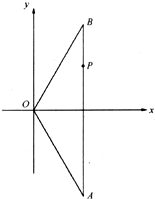（2006•广州一模）如下图，在△OAB中，|OA|=|OB|=4，点P分线段AB所成的比为3：1，以OA、OB所在直线为渐近线的双曲线M恰好经过点P，且离心率为2．
（1）求双曲线M的标准方程；
（2）若直线y=kx+m（k≠0，m≠0）与双曲线M交于不同的两点E、F，且E、F两点都在以Q（0，-3）为圆心的同一圆上，求实数m的取值范围．
（2008•襄阳模拟）在△OAB中，
OA
=(2cosα，2sinα)，
OB
=(5cosβ，5sinβ)，若
OA
•
OB
=-5，则S△OAB=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网