Question

16．△ABC的顶点为A（4，0），B（0，4），C（0，0），则△ABC的内切圆圆心的横坐标是（　　）

• A． 2$\sqrt{2}$-4
• B． 4-2$\sqrt{2}$
• C． 4+2$\sqrt{2}$
• D． 4

Answer 1

分析 设△ABC的内切圆圆心的横坐标是a，则△ABC的内切圆圆心的纵坐标也是a．用截距式求得斜边AB的直线方程，再根据内切圆的圆心到三边距离相等，利用点到直线的距离公式，求得a的值．

解答 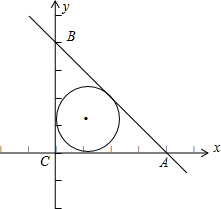解：设△ABC的内切圆圆心的横坐标是a，则△ABC的内切圆圆心的纵坐标也是a，
斜边AB的直线方程为x+y-4=0，如图所示：
则内切圆的半径为|a|=$\frac{|a+a-4|}{\sqrt{2}}$，求得a=4-2$\sqrt{2}$，或a=4+2$\sqrt{2}$（舍去），
故选：B．

点评 本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，体现了数形结合的数学思想，属于基础题．