题目内容
【题目】已知椭圆E:![]() 的一个焦点为
的一个焦点为![]() ,长轴与短轴的比为2:1.直线
,长轴与短轴的比为2:1.直线![]() 与椭圆E交于PQ两点,其中
与椭圆E交于PQ两点,其中![]() 为直线
为直线![]() 的斜率.
的斜率.
(1)求椭圆E的方程;
(2)若以线段PQ为直径的圆过坐标原点O,问:是否存在一个以坐标原点O为圆心的定圆O,不论直线![]() 的斜率
的斜率![]() 取何值,定圆O恒与直线
取何值,定圆O恒与直线![]() 相切?如果存在,求出圆O的方程及实数m的取值范围;如果不存在,请说明理由.
相切?如果存在,求出圆O的方程及实数m的取值范围;如果不存在,请说明理由.
【答案】(1) ![]() (2)存在,
(2)存在,![]() .
.![]() 的取值范围是
的取值范围是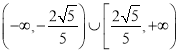
【解析】
(1)根据题意直接计算出![]() 得到答案.
得到答案.
(2)设直线OP的方程为:![]() 点的坐标为
点的坐标为![]() ,则
,则![]() ,联立方程组
,联立方程组 ,设坐标原点O到直线
,设坐标原点O到直线![]() 的距离为d,则有
的距离为d,则有![]() ,得到
,得到![]() ,计算得到答案.
,计算得到答案.
(1)由已知得: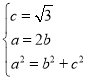 解得:
解得:![]()
![]() 椭圆E的方程为
椭圆E的方程为![]()
(2)假设存在定圆O,不论直线![]() 的斜率k取何值时,定圆O恒与直线
的斜率k取何值时,定圆O恒与直线![]() 相切.
相切.
这时只需证明坐标原点O到直线![]() 的距离为定值即可.
的距离为定值即可.
设直线OP的方程为:![]() 点的坐标为
点的坐标为![]() ,则
,则![]() ,
,
联立方程组
![]() ①
①
![]() 以线段PQ为直径的圆过坐标原点O,
以线段PQ为直径的圆过坐标原点O,
![]() ,直线OQ的方程为:
,直线OQ的方程为:![]()
![]() 在①式中以
在①式中以![]() 换t,得
换t,得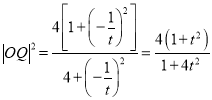 ②
②
又由![]() 知:
知:
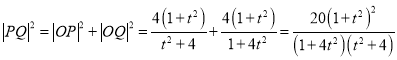
设坐标原点O到直线![]() 的距离为d,则有
的距离为d,则有![]()

又当直线OP与![]() 轴重合时,
轴重合时,![]() 此时
此时![]()
由坐标原点O到直线![]() 的距离
的距离![]() 为定值知,所以存在定圆O,不论直线
为定值知,所以存在定圆O,不论直线![]() 的斜率k取何值时,定圆O恒与直线
的斜率k取何值时,定圆O恒与直线![]() 相切,定圆O的方程为:
相切,定圆O的方程为:![]() .
.
直线![]() 与
与![]() 轴交点为
轴交点为![]() ,且点
,且点![]() 不可能在圆O内,又当k=0时,直线
不可能在圆O内,又当k=0时,直线![]() 与定圆O切于点
与定圆O切于点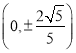 ,所以
,所以![]() 的取值范围是
的取值范围是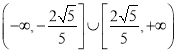

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目