题目内容
设 是夹角为
是夹角为 的单位向量,
的单位向量, 则
则 的取值范围是( )
的取值范围是( )
 是夹角为
是夹角为 的单位向量,
的单位向量, 则
则 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
C
解:根据已知 a • b = 且| a - b | =1,
且| a - b | =1,
由于( a - c )( b + c )=" a" • b + a • c - c • b - c 2=( a - b )• c - ,
,
设 a - b 与 c 的夹角为θ,
则( a - b )• c ="|" a - b || c |cosθ=cosθ∈[-1,1],
故- ≤( a - b )• c -
≤( a - b )• c - ≤
≤ .
.
故答案为[- ,
, ]
]
 且| a - b | =1,
且| a - b | =1,由于( a - c )( b + c )=" a" • b + a • c - c • b - c 2=( a - b )• c -
 ,
,设 a - b 与 c 的夹角为θ,
则( a - b )• c ="|" a - b || c |cosθ=cosθ∈[-1,1],
故-
 ≤( a - b )• c -
≤( a - b )• c - ≤
≤ .
.故答案为[-
 ,
, ]
]
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
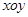 中,若
中,若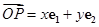 (其中
(其中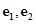 分别是斜坐标系中的
分别是斜坐标系中的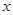 轴和
轴和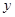 轴正方向上的单位向量,
轴正方向上的单位向量,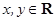 ,
,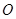 为坐标原点),则称有序数对
为坐标原点),则称有序数对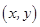 为点
为点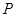 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系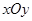 中,若点
中,若点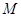 的斜坐标为(1,2),点
的斜坐标为(1,2),点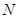 的斜坐标为(3,4),且
的斜坐标为(3,4),且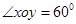 ,则
,则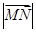 等于 ( )
等于 ( ) 
 所在平面内,点
所在平面内,点 为
为 中点,且满足
中点,且满足 ,设
,设 是
是 上任一点,设向量
上任一点,设向量 ,
, ,向量
,向量 ,若
,若 ,
, ,则
,则 .
. ,
, ,若直线
,若直线 上存在点
上存在点 满足
满足 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



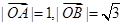 ,
,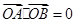 点
点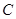 在
在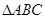 内,且
内,且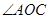
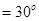 。设
。设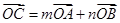
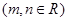 ,则
,则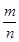 等于
等于


 ,则a.b=( )
,则a.b=( )

 中,
中, 的值等于( )
的值等于( )

 是平面上的两个点,O为坐标原点,若
是平面上的两个点,O为坐标原点,若 ,且
,且 ,则
,则