题目内容
正△ABC与正△BCD所在平面垂直,则二面角ABDC的正弦值为
.
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
分析:取BC的中点O,连接AO,DO,建立空间直角坐标系,确定
为平面BCD的法向量,求出平面ABD的法向量,利用向量的夹角公式,即可得到结论.
| OA |
解答:解:取BC的中点O,连接AO,DO,建立空间直角坐标系,如图所示
设BC=1,则A(0,0,
),B(0,-
,0),D(
,0,0)
∴
=(0,0,
),
=(
,
,0)
由题意,
为平面BCD的法向量
设平面ABD的法向量为
=(x,y,z),则
由
,可得
取x=1,则y=-
,z=1
∴
=(1,-
,1)
∴cos<
,
>=
=
∴sin<
,
>=

设BC=1,则A(0,0,
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| OA |
| ||
| 2 |
| BD |
| ||
| 2 |
| 1 |
| 2 |
由题意,
| OA |
设平面ABD的法向量为
| n |
由
|
|
取x=1,则y=-
| 3 |
∴
| n |
| 3 |
∴cos<
| n |
| OA |
| ||||
|
|
| ||
| 5 |
∴sin<
| n |
| OA |
2
| ||
| 5 |
点评:本题考查二面角的计算,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
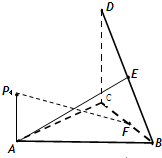 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点. 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:

