题目内容
在平面直角坐标系xOy中,已知圆x2+y2-4x=0的圆心为Q,过点P(0,-4)且斜率为k的直线与圆Q相交于不同的两点A,B。
(1)求k的取值范围;
(2)是否存在常数k,使得向量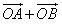 与
与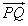 共线?如果存在,求k的值;如果不存在,请说明理由。
共线?如果存在,求k的值;如果不存在,请说明理由。
(1)求k的取值范围;
(2)是否存在常数k,使得向量
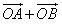 与
与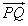 共线?如果存在,求k的值;如果不存在,请说明理由。
共线?如果存在,求k的值;如果不存在,请说明理由。 解:(1)由题意知,圆心Q坐标为(2,0),
直线AB方程为:y=kx-4,
利用圆心到直线的距离公式得:
∴ 。
。
(2)假设存在满足条件的实数k,则设 ,
,
联立 ,得
,得 ,
,
∴ ,且
,且 ,
,
又 ,
, ,
,
∴ ,
,
∴ ,即
,即 ,
,
解得: ,
,
又 ,
,
∴不存在常数k,使得向量 与
与 共线。
共线。
直线AB方程为:y=kx-4,
利用圆心到直线的距离公式得:

∴
 。
。(2)假设存在满足条件的实数k,则设
 ,
,联立
 ,得
,得 ,
,∴
 ,且
,且 ,
,又
 ,
, ,
,∴
 ,
,∴
 ,即
,即 ,
,解得:
 ,
,又
 ,
,∴不存在常数k,使得向量
 与
与 共线。
共线。 
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是